
Sederhanakan bentuk akar berikut merupakan topik penting dalam aljabar. Memahami cara menyederhanakan bentuk akar akan membuka pintu untuk memecahkan berbagai permasalahan matematika, mulai dari soal-soal sederhana hingga persamaan yang lebih kompleks. Artikel ini akan memandu Anda melalui langkah-langkah penyederhanaan, mulai dari pengertian dasar hingga penerapannya dalam berbagai bidang studi.
Kita akan menjelajahi metode penyederhanaan bentuk akar, mencakup penggunaan faktorisasi prima dan sifat-sifat akar. Berbagai contoh soal dengan tingkat kesulitan berbeda akan diberikan, lengkap dengan penyelesaian langkah demi langkah. Selain itu, kita juga akan melihat aplikasi praktis penyederhanaan bentuk akar dalam geometri, fisika, dan penyelesaian persamaan kuadrat.
Pengantar Bentuk Akar

Bentuk akar, dalam matematika, merupakan cara penulisan bilangan yang memuat akar pangkat dua atau lebih tinggi. Secara sederhana, bentuk akar adalah representasi dari suatu bilangan yang jika dipangkatkan dengan bilangan tertentu akan menghasilkan bilangan di dalam tanda akar. Memahami bentuk akar penting untuk menyelesaikan berbagai persamaan matematika dan memecahkan masalah dalam berbagai bidang, seperti geometri dan fisika.
Bentuk akar dapat berupa sederhana atau kompleks. Perbedaannya terletak pada tingkat penyederhanaan dari bentuk akar tersebut. Bentuk akar sederhana telah disederhanakan semaksimal mungkin, sementara bentuk akar kompleks masih dapat disederhanakan lebih lanjut.
Perbedaan Bentuk Akar Sederhana dan Bentuk Akar Kompleks
Berikut ini tabel perbandingan antara bentuk akar sederhana dan bentuk akar yang belum sederhana:
| Bentuk Akar | Bentuk Sederhana | Langkah Penyederhanaan | Keterangan |
|---|---|---|---|
| √12 | 2√3 | √12 = √(4 x 3) = √4 x √3 = 2√3 | Faktorisasi prima dari 12 adalah 2² x 3. Akar kuadrat dari 2² adalah 2, sehingga 2 dikeluarkan dari tanda akar. |
| √50 | 5√2 | √50 = √(25 x 2) = √25 x √2 = 5√2 | Faktorisasi prima dari 50 adalah 5² x 2. Akar kuadrat dari 5² adalah 5, sehingga 5 dikeluarkan dari tanda akar. |
| √75 | 5√3 | √75 = √(25 x 3) = √25 x √3 = 5√3 | Faktorisasi prima dari 75 adalah 5² x 3. Akar kuadrat dari 5² adalah 5, sehingga 5 dikeluarkan dari tanda akar. |
| 3√8 | 6 | 3√8 = 3 x √(2 x 2 x 2) = 3 x 2 = 6 | Akar pangkat tiga dari 8 adalah 2 karena 2 x 2 x 2 = 8. |
Ilustrasi Perbedaan Bentuk Akar Sederhana dan Kompleks
Bayangkan sebuah persegi dengan luas 12 satuan luas. Untuk mencari panjang sisinya, kita perlu menghitung √12. Ini adalah bentuk akar kompleks. Setelah disederhanakan, kita mendapatkan 2√3, yang merupakan bentuk akar sederhana. Bentuk akar kompleks (√12) menunjukkan bahwa kita masih dapat menyederhanakannya lebih lanjut, sementara bentuk akar sederhana (2√3) menunjukkan bahwa penyederhanaan telah dilakukan semaksimal mungkin.
Kita dapat membayangkannya sebagai proses penguraian luas persegi menjadi persegi-persegi yang lebih kecil, hingga mencapai bentuk yang tidak dapat diuraikan lagi menjadi bentuk persegi yang lebih kecil dengan sisi yang merupakan bilangan bulat. Persegi dengan luas 12 dapat dibagi menjadi 4 persegi kecil dengan luas masing-masing 3, sehingga panjang sisinya adalah 2√3. Sedangkan bentuk √12 menunjukkan belum adanya penyederhanaan tersebut.
Bentuk akar kompleks mirip seperti sebuah bangunan yang masih dalam proses konstruksi, sedangkan bentuk akar sederhana adalah bangunan yang telah selesai dan rapi.
Metode Penyederhanaan Bentuk Akar
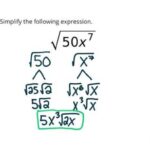
Penyederhanaan bentuk akar merupakan proses untuk menyajikan bentuk akar dalam bentuk paling sederhana, sehingga lebih mudah dipahami dan dioperasikan. Proses ini melibatkan beberapa teknik, termasuk faktorisasi prima dan penggunaan sifat-sifat akar. Dengan memahami teknik-teknik ini, kita dapat menyederhanakan berbagai bentuk akar, termasuk yang melibatkan pecahan dan variabel.
Langkah-Langkah Umum Penyederhanaan Bentuk Akar
Langkah-langkah umum dalam menyederhanakan bentuk akar melibatkan identifikasi faktor-faktor sempurna yang terdapat di dalam akar. Proses ini bertujuan untuk mengeluarkan faktor-faktor tersebut dari dalam tanda akar, sehingga menghasilkan bentuk akar yang lebih sederhana. Kita akan melihat beberapa metode untuk mencapai hal ini.
Penyederhanaan Bentuk Akar dengan Faktorisasi Prima
Metode faktorisasi prima sangat efektif untuk menyederhanakan bentuk akar. Dengan memecah bilangan di dalam akar menjadi faktor-faktor primanya, kita dapat mengidentifikasi faktor-faktor kuadrat sempurna yang dapat dikeluarkan dari dalam tanda akar. Misalnya, untuk menyederhanakan √12, kita dapat melakukan faktorisasi prima: 12 = 2 x 2 x 3 = 2² x 3. Oleh karena itu, √12 dapat disederhanakan menjadi √(2² x 3) = 2√3.
Contoh lain, untuk menyederhanakan √72, kita uraikan 72 menjadi faktor prima: 72 = 2 x 2 x 2 x 3 x 3 = 2² x 2 x 3². Maka √72 = √(2² x 3² x 2) = 2 x 3 √2 = 6√2.
Penyederhanaan Bentuk Akar dengan Sifat-Sifat Akar
Selain faktorisasi prima, kita juga dapat menggunakan sifat-sifat akar untuk menyederhanakan bentuk akar. Beberapa sifat akar yang berguna meliputi: √(a x b) = √a x √b dan √(a/b) = √a / √b, dimana a dan b adalah bilangan real positif. Dengan memanfaatkan sifat-sifat ini, kita dapat memanipulasi bentuk akar untuk mendapatkan bentuk yang lebih sederhana.
Sebagai contoh, untuk menyederhanakan √27/√3, kita dapat menggunakan sifat √(a/b) = √a / √b. Maka √27/√3 = √(27/3) = √9 = 3. Atau, jika kita uraikan √27 = √(3 x 3 x 3) = 3√3, maka √27/√3 = (3√3)/√3 = 3.
Penyederhanaan Bentuk Akar yang Melibatkan Pecahan
Penyederhanaan bentuk akar yang melibatkan pecahan dapat dilakukan dengan cara yang sama seperti penyederhanaan bentuk akar bilangan bulat. Pertama, sederhanakan pecahan di dalam akar jika memungkinkan. Kemudian, gunakan faktorisasi prima atau sifat-sifat akar untuk menyederhanakan bentuk akar tersebut. Pastikan untuk merasionalkan penyebut jika terdapat akar di penyebut.
Contoh: Sederhanakan √(18/8). Pertama, sederhanakan pecahan: 18/8 = 9/4. Kemudian, √(9/4) = √9 / √4 = 3/2.
Penyederhanaan Bentuk Akar yang Mengandung Variabel
Penyederhanaan bentuk akar yang mengandung variabel juga mengikuti prinsip yang sama. Identifikasi faktor-faktor kuadrat sempurna dari koefisien dan variabel. Keluarkan faktor-faktor tersebut dari dalam tanda akar. Ingatlah bahwa √(x²) = |x| untuk semua bilangan real x.
Contoh: Sederhanakan √(16x⁴y²). Kita dapat menulisnya sebagai √(4² x (x²)² x y²) = 4x²|y|.
Contoh Soal dan Penyelesaian
Penyederhanaan bentuk akar merupakan keterampilan penting dalam aljabar. Memahami konsep ini akan memudahkan dalam menyelesaikan berbagai soal matematika, terutama yang berkaitan dengan persamaan dan pertidaksamaan. Berikut beberapa contoh soal penyederhanaan bentuk akar dengan tingkat kesulitan yang bervariasi, disertai penyelesaiannya secara detail.
Soal Penyederhanaan Bentuk Akar Tingkat Mudah
Soal berikut ini bertujuan untuk menguji pemahaman dasar tentang penyederhanaan bentuk akar dengan angka yang relatif sederhana.
- Sederhanakan bentuk akar √12
Penyelesaian:
√12 = √(4 x 3) = √4 x √3 = 2√3
Soal Penyederhanaan Bentuk Akar Tingkat Sedang
Soal ini melibatkan angka yang sedikit lebih kompleks dan membutuhkan pemahaman yang lebih mendalam tentang faktorisasi prima.
- Sederhanakan bentuk akar √75 + √48 – √27
Penyelesaian:
√75 = √(25 x 3) = 5√3
√48 = √(16 x 3) = 4√3
√27 = √(9 x 3) = 3√3
Maka, √75 + √48 – √27 = 5√3 + 4√3 – 3√3 = 6√3
Soal Penyederhanaan Bentuk Akar Tingkat Sulit, Sederhanakan bentuk akar berikut
Soal berikut ini menggabungkan beberapa konsep, termasuk perkalian dan penyederhanaan bentuk akar yang lebih kompleks.
- Sederhanakan bentuk akar √(8/27) x √(3/2)
Penyelesaian:
√(8/27) x √(3/2) = √[(8 x 3) / (27 x 2)] = √(24/54) = √(4/9) = 2/3
Alternatif penyelesaian:
√(8/27) x √(3/2) = (√8/√27) x (√3/√2) = (2√2 / 3√3) x (√3 / √2) = 2/3
Soal Penjumlahan dan Pengurangan Bentuk Akar
Soal ini menguji kemampuan dalam melakukan operasi penjumlahan dan pengurangan bentuk akar yang sejenis.
- Hitunglah 3√2 + 5√2 – √8
Penyelesaian:
Pertama-tama sederhanakan √8 menjadi 2√2.
Maka, 3√2 + 5√2 – 2√2 = 6√2
Aplikasi Penyederhanaan Bentuk Akar: Sederhanakan Bentuk Akar Berikut
Penyederhanaan bentuk akar merupakan keterampilan matematika dasar yang memiliki aplikasi luas di berbagai bidang studi. Kemampuan untuk menyederhanakan bentuk akar memungkinkan perhitungan yang lebih efisien dan interpretasi hasil yang lebih mudah. Berikut beberapa contoh penerapannya dalam berbagai konteks.
Penyederhanaan Bentuk Akar dalam Geometri
Dalam geometri, penyederhanaan bentuk akar sering digunakan untuk menghitung panjang sisi, luas, dan volume bangun geometri. Misalnya, untuk menghitung panjang diagonal suatu persegi dengan sisi sepanjang 2 cm, kita perlu menghitung √(2² + 2²) = √8 = 2√2 cm. Penyederhanaan bentuk akar memudahkan kita dalam memahami dan membandingkan panjang tersebut dengan ukuran lain.
Penerapan Penyederhanaan Bentuk Akar dalam Fisika
Konsep penyederhanaan bentuk akar sering muncul dalam perhitungan fisika, khususnya dalam mekanika dan elektromagnetika. Misalnya, dalam menghitung resultan dua vektor gaya yang membentuk sudut siku-siku, kita seringkali akan mendapatkan hasil yang melibatkan bentuk akar. Penyederhanaan bentuk akar akan memberikan hasil yang lebih ringkas dan mudah diinterpretasikan.
Sebagai contoh, jika dua gaya masing-masing 3 Newton dan 4 Newton bekerja tegak lurus, resultan gaya dapat dihitung menggunakan teorema Pythagoras: √(3² + 4²) = √25 = 5 Newton. Tanpa penyederhanaan, hasil perhitungan akan menjadi lebih rumit.
Penyederhanaan Bentuk Akar dalam Penyelesaian Persamaan Kuadrat
Persamaan kuadrat seringkali menghasilkan solusi yang melibatkan bentuk akar. Penyederhanaan bentuk akar sangat penting untuk menyajikan solusi dalam bentuk yang paling sederhana dan mudah dipahami. Misalnya, persamaan kuadrat x²
-2x – 2 = 0 memiliki solusi x = 1 ± √3. Penyederhanaan bentuk akar √3 memastikan solusi disajikan secara ringkas dan akurat.
Bidang Studi Lain yang Menggunakan Penyederhanaan Bentuk Akar
- Teknik Sipil: Perhitungan struktur bangunan dan jembatan.
- Arsitektur: Perencanaan dan desain bangunan.
- Ilmu Komputer: Grafik komputer dan pemrosesan citra.
- Statistika: Analisis data dan perhitungan probabilitas.
Manfaat Penyederhanaan Bentuk Akar dalam Mempermudah Perhitungan Matematis
Penyederhanaan bentuk akar memiliki manfaat utama dalam mempermudah perhitungan matematis. Bentuk akar yang sederhana memudahkan perhitungan selanjutnya, baik itu penjumlahan, pengurangan, perkalian, maupun pembagian. Selain itu, bentuk akar yang sederhana juga memudahkan dalam membandingkan nilai dan melakukan analisis lebih lanjut. Dengan menyederhanakan bentuk akar, kita dapat menghindari kesalahan perhitungan dan meningkatkan efisiensi dalam menyelesaikan masalah matematika.
Penutup

Dengan memahami konsep dan metode yang diuraikan, Anda kini memiliki kemampuan untuk menyederhanakan berbagai bentuk akar. Kemampuan ini bukan hanya penting untuk menyelesaikan soal-soal matematika, tetapi juga akan membantu Anda dalam memahami konsep-konsep yang lebih lanjut dalam matematika dan ilmu pengetahuan lainnya. Teruslah berlatih dan eksplorasi lebih dalam untuk menguasai topik ini dengan sempurna.
