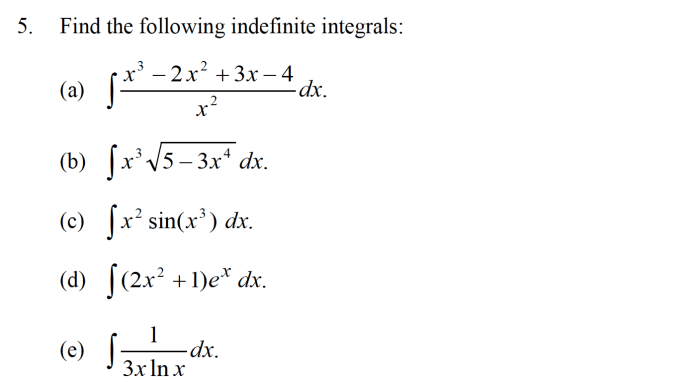Contoh Soal Integral: Panduan Lengkap ini akan memandu Anda menjelajahi dunia menarik kalkulus integral. Mulai dari memahami berbagai jenis soal integral, seperti integral tentu dan tak tentu, hingga menguasai teknik penyelesaian yang beragam, seperti substitusi, parsial, dan trigonometri, panduan ini akan memberikan pemahaman yang komprehensif. Kita akan membahas langkah demi langkah penyelesaian soal, serta mengkaji aplikasi integral dalam berbagai bidang, termasuk perhitungan luas, volume, dan panjang busur.
Selain itu, kita akan mengidentifikasi kesulitan umum yang sering dihadapi dan memberikan strategi efektif untuk mengatasinya. Dengan contoh soal yang terstruktur dan penjelasan yang detail, Anda akan meningkatkan kemampuan dalam menyelesaikan soal integral dengan percaya diri. Mari kita mulai perjalanan menarik ini menuju penguasaan integral!
Jenis-jenis Soal Integral
Integral merupakan konsep fundamental dalam kalkulus yang digunakan untuk menghitung luas daerah, volume benda putar, dan berbagai aplikasi lainnya. Memahami berbagai jenis soal integral dan metode penyelesaiannya sangat penting untuk menguasai kalkulus integral. Berikut ini akan dibahas beberapa jenis soal integral beserta contoh dan penyelesaiannya.
Integral Tentu dan Integral Tak Tentu
Integral tentu dan integral tak tentu merupakan dua jenis integral yang berbeda. Perbedaan utamanya terletak pada batasan integral. Integral tentu memiliki batasan atas dan bawah, menghasilkan nilai numerik yang merepresentasikan luas daerah di bawah kurva. Sedangkan integral tak tentu tidak memiliki batasan, menghasilkan fungsi sebagai hasilnya, yang disebut sebagai antiturunan.
Contoh integral tentu: ∫ 12 2x dx = [x²] 12 = 2²
-1² =
3. Hasilnya adalah nilai numerik
3. Contoh integral tak tentu: ∫ 2x dx = x² + C. Hasilnya adalah fungsi x² + C, dimana C adalah konstanta integrasi.
Integral Substitusi
Metode integral substitusi digunakan untuk menyederhanakan integral yang kompleks dengan mensubstitusikan variabel baru. Metode ini efektif ketika integran mengandung fungsi komposit.
Contoh: Hitunglah ∫ x√(x²+1) dx.
Penyelesaian:
- Misalkan u = x² + 1. Maka du = 2x dx, atau dx = du/(2x).
- Substitusikan u dan du ke dalam integral: ∫ x√u (du/(2x)) = (1/2) ∫ √u du.
- Integralkan terhadap u: (1/2)
(2/3)u3/2 + C = (1/3)u 3/2 + C.
- Substitusikan kembali u = x² + 1: (1/3)(x² + 1) 3/2 + C.
Jadi, hasil integralnya adalah (1/3)(x² + 1) 3/2 + C.
Perbandingan Metode Integral Parsial dan Integral Substitusi
| Metode | Deskripsi | Contoh Soal | Penyelesaian Singkat |
|---|---|---|---|
| Integral Substitusi | Menggunakan substitusi variabel untuk menyederhanakan integran. | ∫ x cos(x²) dx | Misal u = x², du = 2x dx. Maka integral menjadi (1/2)∫ cos(u) du = (1/2)sin(u) + C = (1/2)sin(x²) + C |
| Integral Parsial | Menggunakan rumus ∫ u dv = uv – ∫ v du untuk menyelesaikan integral perkalian dua fungsi. | ∫ x ex dx | Misal u = x, dv = ex dx. Maka du = dx, v = ex. Integral menjadi xex
|
Penyelesaian Soal Integral Trigonometri
Integral trigonometri seringkali melibatkan penggunaan identitas trigonometri untuk menyederhanakan integran. Rumus-rumus identitas trigonometri seperti sin²x + cos²x = 1, sin(2x) = 2sinxcosx, dan lainnya, sangat berguna dalam menyelesaikan integral ini.
Contoh: Hitunglah ∫ sin²x dx.
Penyelesaian:
- Gunakan identitas trigonometri: sin²x = (1 – cos(2x))/2.
- Substitusikan ke dalam integral: ∫ (1 – cos(2x))/2 dx = (1/2) ∫ (1 – cos(2x)) dx.
- Integralkan: (1/2) [x – (1/2)sin(2x)] + C = (1/2)x – (1/4)sin(2x) + C.
Jadi, hasil integralnya adalah (1/2)x – (1/4)sin(2x) + C.
Teknik Penyelesaian Soal Integral

Integral merupakan konsep fundamental dalam kalkulus yang memiliki aplikasi luas dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan statistika. Mempelajari berbagai teknik penyelesaian integral sangat penting untuk memahami dan menyelesaikan masalah yang lebih kompleks. Berikut ini akan diuraikan beberapa teknik umum yang sering digunakan dalam menyelesaikan soal integral, disertai dengan contoh penerapannya.
Integral Parsial
Metode integral parsial merupakan teknik yang efektif untuk menyelesaikan integral yang melibatkan perkalian dua fungsi. Dasar dari metode ini adalah rumus integral parsial: ∫u dv = uv – ∫v du. Langkah-langkah penyelesaiannya meliputi pemilihan fungsi u dan dv yang tepat, penentuan du dan v melalui diferensiasi dan integrasi, dan substitusi ke dalam rumus integral parsial. Pemilihan u dan dv yang tepat seringkali memerlukan pertimbangan dan latihan.
Sebagai contoh, perhatikan integral ∫x sin x dx. Kita dapat memilih u = x dan dv = sin x dx. Dengan demikian, du = dx dan v = -cos x. Substitusi ke dalam rumus integral parsial menghasilkan: ∫x sin x dx = -x cos x + ∫cos x dx = -x cos x + sin x + C, dengan C sebagai konstanta integrasi.
Substitusi Trigonometri
Metode substitusi trigonometri berguna untuk menyelesaikan integral yang mengandung ekspresi yang melibatkan akar kuadrat dari bentuk a²
-x², a² + x², atau x²
-a². Teknik ini melibatkan substitusi variabel x dengan fungsi trigonometri, seperti x = a sin θ, x = a tan θ, atau x = a sec θ, tergantung pada bentuk ekspresi yang ada. Setelah substitusi, integral akan diubah menjadi integral trigonometri yang lebih mudah diselesaikan.
Misalnya, untuk menyelesaikan integral ∫√(a²
-x²) dx, kita dapat menggunakan substitusi x = a sin θ. Maka dx = a cos θ dθ dan √(a²
-x²) = √(a²
-a² sin² θ) = a cos θ. Integral tersebut kemudian berubah menjadi ∫a² cos² θ dθ, yang dapat diselesaikan menggunakan rumus trigonometri dan menghasilkan solusi berupa fungsi trigonometri yang dapat diubah kembali ke dalam variabel x.
Pecahan Parsial
Teknik pecahan parsial digunakan untuk mengintegralkan fungsi rasional, yaitu fungsi yang berbentuk pecahan dengan polinomial di pembilang dan penyebut. Langkah awal adalah memfaktorkan penyebut menjadi faktor-faktor linear atau kuadrat. Kemudian, fungsi rasional diuraikan menjadi penjumlahan pecahan-pecahan yang lebih sederhana, dengan pembilang konstanta atau linear dan penyebut yang merupakan faktor-faktor penyebut semula. Setiap pecahan sederhana kemudian dapat diintegralkan secara terpisah.
Sebagai ilustrasi, perhatikan integral ∫(2x + 1)/(x² + x) dx. Penyebut dapat difaktorkan menjadi x(x+1). Dengan metode pecahan parsial, fungsi tersebut dapat diuraikan menjadi A/x + B/(x+1). Menentukan nilai A dan B melalui aljabar, kemudian mengintegralkan setiap pecahan menghasilkan solusi berupa kombinasi logaritma natural.
Contoh Soal Gabungan Teknik
Terkadang, menyelesaikan suatu integral membutuhkan lebih dari satu teknik. Perhatikan integral ∫x²/(x² + 1) dx. Integral ini dapat diselesaikan dengan membagi x² dengan (x²+1) sehingga diperoleh 1 – 1/(x²+1). Integral dari 1 mudah, yaitu x. Integral dari 1/(x²+1) adalah arctan(x).
Jadi, solusi integral tersebut adalah x – arctan(x) + C.
Ringkasan Teknik Penyelesaian Integral
| Teknik | Kelebihan | Kekurangan |
|---|---|---|
| Integral Parsial | Efektif untuk integral perkalian dua fungsi | Membutuhkan pemilihan u dan dv yang tepat |
| Substitusi Trigonometri | Berguna untuk integral yang melibatkan akar kuadrat tertentu | Membutuhkan transformasi trigonometri |
| Pecahan Parsial | Berguna untuk integral fungsi rasional | Membutuhkan pemfaktoran penyebut dan aljabar |
Aplikasi Soal Integral
Integral, sebagai konsep inti dalam kalkulus, memiliki penerapan luas dalam berbagai bidang, terutama dalam menghitung besaran geometris dan fisika. Pemahaman integral memungkinkan kita untuk menyelesaikan permasalahan yang kompleks yang sulit dipecahkan dengan metode aljabar sederhana. Berikut beberapa contoh penerapan integral dalam konteks yang lebih spesifik.
Menghitung Luas Daerah di Bidang Datar
Integral tentu dapat digunakan untuk menghitung luas daerah yang dibatasi oleh kurva dan sumbu x (atau sumbu y). Misalnya, untuk mencari luas daerah yang dibatasi oleh kurva y = x² dan sumbu x antara x = 0 dan x = 1, kita dapat menghitung integral tentu ∫₀¹ x² dx. Hasil integral ini akan memberikan nilai luas daerah tersebut.
Menghitung Volume Benda Putar
Metode integral juga berperan penting dalam menentukan volume benda putar. Bayangkan sebuah kurva yang diputar mengelilingi sumbu x. Volume benda putar yang dihasilkan dapat dihitung menggunakan integral tentu yang melibatkan rumus khusus. Sebagai contoh, jika kurva y = √x diputar mengelilingi sumbu x dari x = 0 hingga x = 1, maka volume benda putar yang terbentuk dapat dihitung dengan rumus integral tertentu yang melibatkan fungsi tersebut.
Menghitung Panjang Busur Kurva
Integral tidak hanya berguna untuk menghitung luas dan volume, tetapi juga panjang busur suatu kurva. Rumus integral untuk menghitung panjang busur melibatkan turunan pertama fungsi yang merepresentasikan kurva tersebut. Misalnya, untuk mencari panjang busur kurva y = x³/2 dari titik (0,0) sampai (1,1/2), kita perlu menghitung integral tertentu yang melibatkan akar kuadrat dari 1 + (dy/dx)².
Menghitung Kerja yang Dilakukan oleh Suatu Gaya
Integral memiliki peranan krusial dalam fisika, khususnya dalam menghitung kerja yang dilakukan oleh suatu gaya yang berubah-ubah terhadap perpindahan. Misalkan kita memiliki kurva gaya F(x) terhadap perpindahan x. Kurva ini dapat berupa kurva linier, parabola, atau bentuk lainnya tergantung pada sifat gaya. Kerja total yang dilakukan gaya tersebut dari titik x₁ ke x₂ dapat dihitung dengan mengintegralkan fungsi gaya terhadap perpindahan, yaitu ∫ₓ₁ˣ₂ F(x) dx.
Jika kurva gaya berbentuk parabola misalnya, maka integral tentu dari fungsi parabola tersebut terhadap x dari x₁ hingga x₂ akan menghasilkan nilai kerja total.
Penerapan Integral dalam Bidang Fisika dan Teknik
Integral merupakan alat yang sangat ampuh dalam berbagai aplikasi fisika dan teknik. Dari menghitung momen inersia suatu benda hingga menganalisis aliran fluida, integral memberikan solusi numerik untuk masalah-masalah yang kompleks. Penggunaan integral dalam dinamika fluida, mekanika, dan elektromagnetika sangatlah luas dan fundamental.
Soal Integral dan Rumus-rumus Terkait: Contoh Soal Integral
Integral merupakan konsep kunci dalam kalkulus yang berkaitan dengan penjumlahan sejumlah tak hingga. Memahami rumus-rumus integral dasar sangat penting untuk menyelesaikan berbagai permasalahan matematika dan aplikasi di bidang lain seperti fisika dan teknik. Berikut ini akan dijabarkan beberapa rumus integral penting, penggunaan pada fungsi trigonometri, dan contoh penerapannya.
Rumus-rumus Integral Dasar
Menguasai rumus integral dasar merupakan langkah awal yang krusial dalam perhitungan integral. Rumus-rumus ini menjadi landasan untuk menyelesaikan integral yang lebih kompleks. Pemahaman yang baik terhadap rumus-rumus ini akan mempermudah proses penyelesaian soal.
- ∫ x n dx = (x n+1)/(n+1) + C, dengan n ≠ -1
- ∫ 1/x dx = ln|x| + C
- ∫ e x dx = e x + C
- ∫ a x dx = (a x)/ln(a) + C
- ∫ sin(x) dx = -cos(x) + C
- ∫ cos(x) dx = sin(x) + C
Rumus Integral yang Sering Digunakan
Beberapa rumus integral tertentu lebih sering muncul dalam penyelesaian soal dibandingkan yang lain. Mempelajari dan memahami rumus-rumus ini akan meningkatkan efisiensi dan kecepatan dalam menyelesaikan soal integral.
- Integral substitusi: Teknik ini digunakan untuk menyederhanakan integral dengan mengubah variabel. Misalnya, integral dari bentuk ∫f(g(x))g'(x)dx dapat disederhanakan dengan substitusi u = g(x).
- Integral parsial: Metode ini digunakan untuk menyelesaikan integral perkalian dua fungsi. Rumusnya adalah ∫udv = uv – ∫vdu.
- Integral trigonometri: Rumus-rumus integral trigonometri, seperti yang akan dijelaskan selanjutnya, sering digunakan dalam berbagai aplikasi.
Penggunaan Rumus Integral untuk Fungsi Trigonometri
Fungsi trigonometri sering muncul dalam berbagai permasalahan, baik dalam matematika murni maupun terapan. Rumus-rumus integral untuk fungsi trigonometri merupakan bagian penting dalam menyelesaikan soal-soal yang melibatkan fungsi-fungsi ini.
- ∫ sin 2(x) dx = (x/2)
-(sin(2x)/4) + C - ∫ cos 2(x) dx = (x/2) + (sin(2x)/4) + C
- ∫ tan(x) dx = ln|sec(x)| + C
- ∫ cot(x) dx = ln|sin(x)| + C
- ∫ sec(x) dx = ln|sec(x) + tan(x)| + C
- ∫ csc(x) dx = ln|csc(x)
-cot(x)| + C
Tabel Rumus Integral dan Contoh Penggunaan
Tabel berikut merangkum beberapa rumus integral beserta contoh penggunaannya. Melihat contoh penerapan langsung akan mempermudah pemahaman dan membantu dalam menyelesaikan soal-soal integral.
| Rumus | Contoh | Penyelesaian |
|---|---|---|
| ∫ x2 dx | Hitunglah ∫ x2 dx dari batas bawah 0 sampai batas atas 2 | [(x3)/3] dari 0 sampai 2 = (8/3) – 0 = 8/3 |
| ∫ ex dx | Hitunglah ∫ ex dx dari batas bawah 1 sampai batas atas 3 | [ex] dari 1 sampai 3 = e3 – e |
| ∫ sin(x) dx | Hitunglah ∫ sin(x) dx dari batas bawah 0 sampai batas atas π/2 | [-cos(x)] dari 0 sampai π/2 = -cos(π/2) + cos(0) = 1 |
Contoh Soal Integral
Berikut contoh soal yang melibatkan penggunaan tabel integral di atas dan memerlukan pemahaman konsep integral. Dengan memahami contoh ini, diharapkan dapat meningkatkan kemampuan dalam menyelesaikan soal integral yang lebih kompleks.
Tentukan nilai dari ∫ 01 (x² + e x + sin(x)) dx
Penyelesaian: Integral tersebut dapat dipecah menjadi tiga integral terpisah:
∫01 x² dx + ∫ 01 e x dx + ∫ 01 sin(x) dx
Dengan menggunakan rumus-rumus integral dasar dan tabel di atas, kita dapat menghitung masing-masing integral dan menjumlahkannya untuk mendapatkan hasil akhir.
Kesulitan dalam Menyelesaikan Soal Integral dan Solusinya

Integral, sebagai konsep inti dalam kalkulus, seringkali menjadi tantangan bagi banyak siswa. Memahami konsep dasar hingga mengaplikasikannya dalam soal-soal yang kompleks membutuhkan latihan dan strategi yang tepat. Artikel ini akan mengidentifikasi beberapa kesulitan umum dalam menyelesaikan soal integral dan memberikan solusi praktis untuk mengatasinya.
Kesulitan Umum dalam Menyelesaikan Soal Integral
Beberapa kesulitan yang sering dihadapi siswa dalam menyelesaikan soal integral antara lain kesulitan dalam memilih teknik integrasi yang tepat, kesalahan dalam manipulasi aljabar, dan kurangnya pemahaman konseptual yang mendalam. Kesulitan lain termasuk memahami batas integrasi dan penerapan teorema-teorema integral. Kurangnya latihan soal juga menjadi faktor penyebab kesulitan dalam menyelesaikan soal integral yang lebih kompleks.
Strategi Mengatasi Kesulitan dalam Menyelesaikan Soal Integral
Untuk mengatasi kesulitan tersebut, beberapa strategi dapat diterapkan. Penting untuk memahami konsep dasar integral terlebih dahulu, termasuk definisi integral, teorema fundamental kalkulus, dan berbagai teknik integrasi seperti substitusi, parsial, dan trigonometri. Latihan soal secara rutin dan terstruktur sangat penting untuk meningkatkan pemahaman dan kemampuan dalam menyelesaikan soal integral. Memulai dari soal-soal dasar dan secara bertahap meningkatkan kompleksitas soal akan membantu membangun fondasi yang kuat.
Langkah-langkah Sistematis Memecahkan Soal Integral Kompleks, Contoh soal integral
- Identifikasi tipe integral: Tentukan jenis integral yang dihadapi (tak tentu atau tentu).
- Pilih teknik integrasi yang tepat: Perhatikan bentuk integran dan pilih teknik yang paling sesuai (substitusi, parsial, trigonometri, dll.).
- Lakukan manipulasi aljabar: Sederhanakan integran jika perlu sebelum melakukan integrasi.
- Terapkan teknik integrasi yang dipilih: Lakukan integrasi sesuai dengan teknik yang telah dipilih, perhatikan detail perhitungan.
- Verifikasi hasil: Periksa kembali hasil integrasi dengan cara mendiferensiasikan hasil tersebut. Jika hasilnya sama dengan integran awal, maka integrasi telah dilakukan dengan benar.
- Tentukan nilai integral tentu (jika ada): Jika integralnya tentu, substitusikan batas integrasi untuk mendapatkan nilai numerik integral.
Tips dan Trik Menyelesaikan Soal Integral dengan Efisien
Mulailah dengan memahami konsep dasar integral dan berbagai teknik integrasi. Latihan soal secara konsisten sangat penting. Jangan ragu untuk mencari bantuan dari tutor atau teman jika mengalami kesulitan. Ingatlah bahwa pemahaman konseptual yang kuat adalah kunci untuk menyelesaikan soal integral dengan efisien dan akurat. Jangan takut untuk mencoba berbagai pendekatan dan jangan menyerah jika menemukan soal yang sulit.
Sumber Daya Tambahan untuk Belajar Integral
- Buku Kalkulus: Banyak buku teks kalkulus yang tersedia, baik dalam versi cetak maupun digital, yang membahas integral secara detail. Carilah buku yang sesuai dengan tingkat pemahaman Anda.
- Website Pendidikan: Beberapa website pendidikan menyediakan materi pembelajaran integral, contoh soal, dan latihan soal interaktif. Contohnya Khan Academy dan MIT OpenCourseWare.
- Video Pembelajaran: Video pembelajaran di platform seperti YouTube dapat membantu dalam memahami konsep integral yang rumit. Carilah video yang dibuat oleh pengajar yang terpercaya dan berpengalaman.
Terakhir
Memahami konsep integral merupakan kunci untuk menguasai berbagai bidang dalam matematika dan ilmu terapan. Melalui pemahaman yang mendalam tentang jenis-jenis integral, teknik penyelesaian, dan aplikasinya, Anda akan mampu menyelesaikan soal-soal integral dengan lebih efektif dan efisien. Panduan ini telah memberikan landasan yang kuat untuk melanjutkan eksplorasi lebih lanjut dalam dunia kalkulus integral. Semoga panduan ini bermanfaat dan membantu Anda mencapai pemahaman yang lebih baik.