- Pengertian Korelasi
- Metode Analisis Korelasi
- Interpretasi Hasil Analisis Korelasi
-
Penerapan Analisis Korelasi: Analisis Korelasi Adalah
- Contoh Penerapan Analisis Korelasi di Bidang Ekonomi
- Contoh Penerapan Analisis Korelasi di Bidang Kesehatan
- Contoh Penerapan Analisis Korelasi di Bidang Pendidikan
- Skenario Penelitian Menggunakan Analisis Korelasi
- Perbedaan Analisis Korelasi dan Analisis Regresi
- Penggunaan Analisis Korelasi untuk Variabel Kompleks, Analisis korelasi adalah
- Penutup
Analisis korelasi adalah metode statistik yang digunakan untuk mengukur kekuatan dan arah hubungan antara dua variabel atau lebih. Bayangkan Anda ingin mengetahui apakah ada hubungan antara jumlah jam belajar dengan nilai ujian. Atau mungkin ingin melihat apakah ada korelasi antara tingkat pendapatan dengan tingkat kebahagiaan. Analisis korelasi dapat membantu menjawab pertanyaan-pertanyaan seperti ini dengan memberikan gambaran kuantitatif tentang hubungan tersebut.
Metode ini sangat berguna dalam berbagai bidang, mulai dari ilmu sosial hingga ilmu alam, membantu kita memahami pola dan tren dalam data.
Pemahaman mendalam tentang analisis korelasi melibatkan pemahaman berbagai jenis korelasi (positif, negatif, dan nol), serta metode perhitungan seperti metode Pearson. Selain itu, penting untuk memahami bagaimana menginterpretasikan hasil analisis, termasuk nilai koefisien korelasi dan signifikansi statistik, serta batasannya. Analisis ini tidak hanya mengungkap seberapa kuat hubungan antara variabel, tetapi juga arah hubungan tersebut. Dengan demikian, kita dapat membuat prediksi dan pengambilan keputusan yang lebih baik berdasarkan data yang ada.
Pengertian Korelasi

Analisis korelasi merupakan metode statistik yang digunakan untuk mengukur kekuatan dan arah hubungan antara dua variabel atau lebih. Analisis ini tidak membuktikan sebab-akibat, melainkan hanya menunjukkan seberapa erat hubungan antara variabel-variabel tersebut. Dengan kata lain, korelasi menunjukkan sejauh mana perubahan pada satu variabel diiringi oleh perubahan pada variabel lainnya.
Pemahaman tentang korelasi sangat penting dalam berbagai bidang, mulai dari penelitian ilmiah hingga pengambilan keputusan bisnis. Dengan mengetahui hubungan antara variabel, kita dapat membuat prediksi yang lebih akurat dan mengambil langkah-langkah yang lebih efektif.
Contoh Kasus Korelasi dalam Kehidupan Sehari-hari
Bayangkan Anda ingin mengetahui apakah ada hubungan antara jumlah jam belajar dan nilai ujian siswa. Anda dapat mengumpulkan data nilai ujian dan jumlah jam belajar dari sejumlah siswa, kemudian menganalisisnya menggunakan metode korelasi. Jika ditemukan korelasi positif yang kuat, ini menunjukkan bahwa semakin banyak siswa belajar, semakin tinggi nilai ujian yang mereka peroleh. Contoh lain, korelasi antara jumlah es krim yang terjual dan jumlah kasus sengatan matahari mungkin menunjukkan hubungan positif, meskipun tidak berarti es krim menyebabkan sengatan matahari (hubungannya mungkin karena keduanya meningkat pada hari-hari panas).
Jenis-jenis Korelasi
Terdapat tiga jenis korelasi utama: positif, negatif, dan nol. Masing-masing jenis korelasi memiliki karakteristik dan implikasi yang berbeda dalam interpretasinya.
Tabel Perbandingan Jenis Korelasi
| Jenis Korelasi | Definisi | Contoh | Interpretasi |
|---|---|---|---|
| Positif | Ketika satu variabel meningkat, variabel lain juga meningkat. | Hubungan antara tinggi badan dan berat badan pada orang dewasa. | Indikasi hubungan searah yang kuat antara kedua variabel. |
| Negatif | Ketika satu variabel meningkat, variabel lain menurun. | Hubungan antara jumlah jam bermain game dan nilai ujian (mungkin). | Indikasi hubungan berlawanan arah antara kedua variabel. |
| Nol | Tidak ada hubungan yang signifikan antara kedua variabel. | Hubungan antara ukuran sepatu dan tingkat kecerdasan. | Tidak ada keterkaitan yang dapat diidentifikasi antara kedua variabel. |
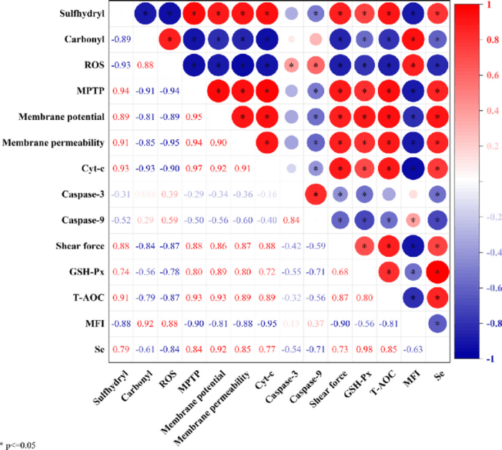
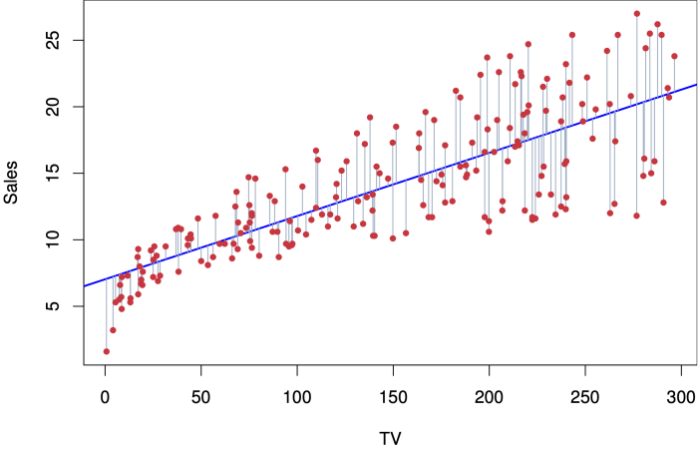
Ilustrasi Grafik Korelasi
Korelasi positif digambarkan sebagai titik-titik data yang cenderung membentuk garis naik dari kiri bawah ke kanan atas. Semakin rapat titik-titik data tersebut berkumpul di sekitar garis, semakin kuat korelasinya. Korelasi negatif ditunjukkan dengan titik-titik data yang membentuk garis menurun dari kiri atas ke kanan bawah. Kembali, kerapatan titik-titik data menandakan kekuatan korelasi. Sedangkan korelasi nol ditunjukkan oleh titik-titik data yang tersebar acak tanpa membentuk pola garis yang jelas, menunjukkan tidak adanya hubungan yang signifikan antara kedua variabel.
Metode Analisis Korelasi
Analisis korelasi merupakan metode statistik yang digunakan untuk mengukur kekuatan dan arah hubungan antara dua variabel atau lebih. Pemahaman tentang korelasi sangat penting dalam berbagai bidang, mulai dari penelitian ilmiah hingga pengambilan keputusan bisnis. Metode yang paling umum digunakan adalah korelasi Pearson, namun terdapat metode lain yang dapat dipilih tergantung pada jenis data dan tujuan analisis.
Langkah-Langkah Analisis Korelasi Pearson
Analisis korelasi Pearson digunakan untuk mengukur hubungan linear antara dua variabel kontinu. Berikut langkah-langkahnya:
- Kumpulkan data untuk kedua variabel yang akan dianalisis. Pastikan data berdistribusi normal atau mendekati normal.
- Hitung rata-rata (mean) dan standar deviasi untuk masing-masing variabel.
- Hitung kovariansi antara kedua variabel. Kovariansi mengukur seberapa besar kedua variabel berubah bersamaan.
- Hitung koefisien korelasi Pearson (r) menggunakan rumus:
r = Σ[(xi - x̄)(yi - ȳ)] / √[Σ(xi - x̄)²Σ(yi - ȳ)²], dimana xi dan yi adalah nilai observasi masing-masing variabel, x̄ dan ȳ adalah rata-rata masing-masing variabel, dan Σ menunjukkan penjumlahan. - Interpretasikan nilai koefisien korelasi. Nilai r berkisar antara -1 hingga +1. Nilai mendekati +1 menunjukkan korelasi positif yang kuat, nilai mendekati -1 menunjukkan korelasi negatif yang kuat, dan nilai mendekati 0 menunjukkan tidak ada korelasi.
- Uji signifikansi statistik koefisien korelasi untuk menentukan apakah hubungan tersebut signifikan secara statistik atau hanya kebetulan.
Perhitungan Koefisien Korelasi Pearson
Berikut contoh perhitungan koefisien korelasi Pearson dengan data sederhana:
| X (Jam Belajar) | Y (Nilai Ujian) |
|---|---|
| 2 | 60 |
| 4 | 70 |
| 6 | 80 |
| 8 | 90 |
| 10 | 100 |
Langkah-langkah perhitungan:
- Hitung rata-rata X (x̄) = (2+4+6+8+10)/5 = 6
- Hitung rata-rata Y (ȳ) = (60+70+80+90+100)/5 = 80
- Hitung Σ[(xi – x̄)(yi – ȳ)] = (2-6)(60-80) + (4-6)(70-80) + (6-6)(80-80) + (8-6)(90-80) + (10-6)(100-80) = 80
- Hitung Σ(xi – x̄)² = (2-6)² + (4-6)² + (6-6)² + (8-6)² + (10-6)² = 40
- Hitung Σ(yi – ȳ)² = (60-80)² + (70-80)² + (80-80)² + (90-80)² + (100-80)² = 800
- Hitung koefisien korelasi Pearson (r) = 80 / √(40 – 800) = 1
Dalam contoh ini, nilai r = 1 menunjukkan korelasi positif yang sempurna antara jam belajar dan nilai ujian.
Metode Analisis Korelasi Selain Pearson
Selain korelasi Pearson, terdapat metode lain yang dapat digunakan untuk menganalisis korelasi, tergantung pada jenis data dan asumsi yang terpenuhi. Dua metode yang umum digunakan adalah:
- Korelasi Spearman: Digunakan untuk mengukur hubungan monotonik antara dua variabel ordinal atau variabel kontinu yang tidak memenuhi asumsi normalitas. Korelasi Spearman mengukur seberapa baik hubungan antara peringkat dua variabel, bukan nilai numeriknya.
- Korelasi Kendall: Mirip dengan korelasi Spearman, metode ini juga digunakan untuk data ordinal atau data kontinu yang tidak terdistribusi normal. Namun, Korelasi Kendall lebih robust terhadap outlier dibandingkan Spearman.
Perbedaan utama antara korelasi Pearson dan Spearman/Kendall terletak pada jenis data yang dianalisis dan asumsi yang dibutuhkan. Pearson mengasumsikan hubungan linear dan data normal, sedangkan Spearman dan Kendall lebih fleksibel untuk data non-normal dan hubungan monotonik.
Interpretasi Hasil Analisis Korelasi
Interpretasi hasil analisis korelasi melibatkan dua aspek utama: nilai koefisien korelasi dan signifikansi statistik.
- Nilai Koefisien Korelasi (r): Menunjukkan kekuatan dan arah hubungan. Nilai mendekati +1 menunjukkan korelasi positif yang kuat, nilai mendekati -1 menunjukkan korelasi negatif yang kuat, dan nilai mendekati 0 menunjukkan tidak ada korelasi.
- Signifikansi Statistik: Menunjukkan apakah hubungan yang diamati signifikan secara statistik atau hanya terjadi secara kebetulan. Hal ini biasanya diuji menggunakan uji t atau uji-F, dan hasilnya dinyatakan dalam nilai p-value. Nilai p-value yang kurang dari tingkat signifikansi (misalnya, 0.05) menunjukkan bahwa hubungan tersebut signifikan secara statistik.
Interpretasi Hasil Analisis Korelasi

Setelah melakukan analisis korelasi, langkah selanjutnya adalah menginterpretasikan hasil yang diperoleh. Interpretasi ini melibatkan pemahaman nilai koefisien korelasi, signifikansi statistik, dan batasan-batasan dalam penarikan kesimpulan. Interpretasi yang tepat akan memberikan pemahaman yang akurat tentang hubungan antara variabel yang diteliti.
Nilai Koefisien Korelasi
Nilai koefisien korelasi (r) berkisar antara -1 hingga +1. Nilai mendekati +1 menunjukkan korelasi positif yang kuat, nilai mendekati -1 menunjukkan korelasi negatif yang kuat, sedangkan nilai mendekati 0 menunjukkan tidak adanya korelasi atau korelasi yang sangat lemah. Sebagai contoh, r = 0.8 menunjukkan korelasi positif yang kuat, artinya jika satu variabel meningkat, variabel lainnya cenderung meningkat pula.
Sebaliknya, r = -0.5 menunjukkan korelasi negatif sedang, artinya jika satu variabel meningkat, variabel lainnya cenderung menurun. Nilai r = 0.1 menunjukkan korelasi yang sangat lemah, hampir tidak ada hubungan antara kedua variabel.
Contoh Interpretasi Hasil Analisis Korelasi
Misalnya, dalam penelitian tentang pengaruh lama belajar terhadap nilai ujian, diperoleh nilai koefisien korelasi r = 0.7 dengan signifikansi p < 0.05. Hal ini mengindikasikan adanya korelasi positif yang kuat dan signifikan secara statistik antara lama belajar dan nilai ujian. Artinya, semakin lama siswa belajar, semakin tinggi nilai ujian yang cenderung diperoleh. Namun, perlu diingat bahwa korelasi ini tidak serta merta membuktikan bahwa lama belajar -menyebabkan* nilai ujian tinggi. Faktor lain juga dapat mempengaruhi nilai ujian.
Pentingnya Signifikansi Statistik
Signifikansi statistik (biasanya dilambangkan dengan p-value) menunjukkan probabilitas bahwa korelasi yang diamati terjadi secara kebetulan. Nilai p yang rendah (misalnya, p < 0.05) menunjukkan bahwa korelasi tersebut signifikan secara statistik, artinya kecil kemungkinan korelasi tersebut terjadi secara kebetulan. Dengan kata lain, hasil analisis korelasi dapat diandalkan dan bukan hanya karena faktor acak. Jika nilai p tinggi, maka korelasi yang ditemukan mungkin tidak signifikan secara statistik, dan kesimpulan yang diambil harus lebih hati-hati.
Batasan Interpretasi Korelasi
Korelasi tidak sama dengan kausalitas. Hanya karena dua variabel berkorelasi tidak berarti satu variabel menyebabkan variabel lainnya. Hubungan tersebut mungkin disebabkan oleh variabel ketiga yang tidak diamati (variabel pencampur), atau mungkin hanya kebetulan.
Potensi Bias dan Kesalahan Umum
Beberapa potensi bias dan kesalahan umum dalam interpretasi hasil analisis korelasi antara lain:
- Menarik kesimpulan kausalitas dari korelasi.
- Mengabaikan variabel pencampur yang mungkin mempengaruhi hubungan antara dua variabel.
- Menginterpretasikan korelasi yang lemah sebagai bukti hubungan yang signifikan.
- Tidak mempertimbangkan konteks penelitian dan karakteristik data.
- Menafsirkan korelasi linier untuk hubungan non-linier.
Penerapan Analisis Korelasi: Analisis Korelasi Adalah

Analisis korelasi merupakan alat statistik yang ampuh untuk mengungkap hubungan antara dua atau lebih variabel. Kemampuannya untuk mengidentifikasi pola dan tren membuatnya sangat berguna dalam berbagai disiplin ilmu. Berikut beberapa contoh penerapan analisis korelasi di berbagai bidang.
Contoh Penerapan Analisis Korelasi di Bidang Ekonomi
Dalam ekonomi, analisis korelasi sering digunakan untuk menganalisis hubungan antara berbagai faktor ekonomi. Misalnya, kita dapat menyelidiki hubungan antara tingkat suku bunga dan investasi. Variabel yang diukur adalah tingkat suku bunga (misalnya, suku bunga acuan Bank Sentral) dan jumlah investasi (misalnya, total investasi sektor swasta). Analisis korelasi akan menunjukkan seberapa kuat hubungan antara kedua variabel tersebut, apakah positif (peningkatan suku bunga diikuti peningkatan investasi), negatif (peningkatan suku bunga diikuti penurunan investasi), atau tidak ada korelasi sama sekali.
Hasil analisis ini dapat membantu pembuat kebijakan ekonomi dalam merumuskan strategi yang tepat.
Contoh Penerapan Analisis Korelasi di Bidang Kesehatan
Di bidang kesehatan, analisis korelasi dapat digunakan untuk mengidentifikasi hubungan antara faktor gaya hidup dan risiko penyakit tertentu. Sebagai contoh, kita dapat meneliti hubungan antara jumlah konsumsi gula harian dan tingkat kejadian diabetes tipe 2. Variabel yang diukur adalah jumlah konsumsi gula harian (dalam gram) dan persentase kejadian diabetes tipe 2 dalam suatu populasi. Analisis korelasi akan menunjukkan apakah ada hubungan signifikan antara kedua variabel tersebut, dan seberapa kuat hubungan tersebut.
Informasi ini berguna untuk kampanye kesehatan publik dan pengembangan strategi pencegahan penyakit.
Contoh Penerapan Analisis Korelasi di Bidang Pendidikan
Dalam bidang pendidikan, analisis korelasi dapat digunakan untuk mengevaluasi hubungan antara waktu belajar dan nilai ujian. Misalnya, kita dapat meneliti hubungan antara jumlah jam belajar per minggu dan nilai ujian akhir siswa. Variabel yang diukur adalah jumlah jam belajar per minggu dan nilai ujian akhir (misalnya, dalam skala 0-100). Analisis korelasi akan menunjukkan seberapa kuat hubungan antara waktu belajar dan prestasi akademik.
Hasil ini dapat membantu guru dalam memahami faktor-faktor yang mempengaruhi keberhasilan belajar siswa dan merancang strategi pembelajaran yang lebih efektif.
Skenario Penelitian Menggunakan Analisis Korelasi
Sebuah penelitian ingin mengkaji hubungan antara tingkat stres dan produktivitas kerja pada karyawan di sebuah perusahaan. Pertanyaan penelitiannya adalah: Apakah ada korelasi antara tingkat stres dan produktivitas kerja? Variabel yang diukur adalah tingkat stres (diukur menggunakan kuesioner standar) dan produktivitas kerja (diukur berdasarkan output kerja per minggu). Analisis korelasi akan digunakan untuk menguji hipotesis adanya korelasi negatif antara tingkat stres dan produktivitas kerja (yaitu, semakin tinggi tingkat stres, semakin rendah produktivitas kerja).
Perbedaan Analisis Korelasi dan Analisis Regresi
Analisis korelasi mengukur kekuatan dan arah hubungan antara dua atau lebih variabel, tanpa mengasumsikan adanya hubungan sebab-akibat. Analisis regresi, di sisi lain, tidak hanya mengukur kekuatan dan arah hubungan, tetapi juga memodelkan hubungan tersebut untuk memprediksi nilai variabel dependen berdasarkan nilai variabel independen. Analisis regresi mengasumsikan adanya hubungan sebab-akibat antara variabel independen dan dependen.
Penggunaan Analisis Korelasi untuk Variabel Kompleks, Analisis korelasi adalah
Analisis korelasi dapat digunakan untuk mengidentifikasi hubungan antara variabel-variabel yang kompleks dengan menggunakan teknik-teknik statistik multivariat seperti analisis korelasi parsial atau analisis faktor. Misalnya, untuk meneliti pengaruh beberapa faktor (misalnya, tingkat pendidikan, pendapatan, dan status kesehatan) terhadap kepuasan hidup, analisis korelasi parsial dapat digunakan untuk mengisolasi pengaruh masing-masing faktor secara independen, sambil mengendalikan pengaruh faktor lainnya. Analisis faktor dapat digunakan untuk mengidentifikasi faktor-faktor laten (tersembunyi) yang mendasari sejumlah variabel yang diamati.
Penutup
Analisis korelasi terbukti menjadi alat yang ampuh dalam mengungkap hubungan tersembunyi antara variabel-variabel dalam berbagai konteks. Meskipun tidak menunjukkan kausalitas, pemahaman tentang kekuatan dan arah hubungan antar variabel memberikan wawasan berharga untuk penelitian dan pengambilan keputusan. Dengan memahami metode perhitungan, interpretasi hasil, dan batasannya, kita dapat memanfaatkan analisis korelasi secara efektif untuk menguji hipotesis dan memahami dunia di sekitar kita dengan lebih baik.
Kemampuan untuk mengidentifikasi hubungan-hubungan ini membuka jalan untuk pengembangan strategi dan solusi yang lebih tepat sasaran.