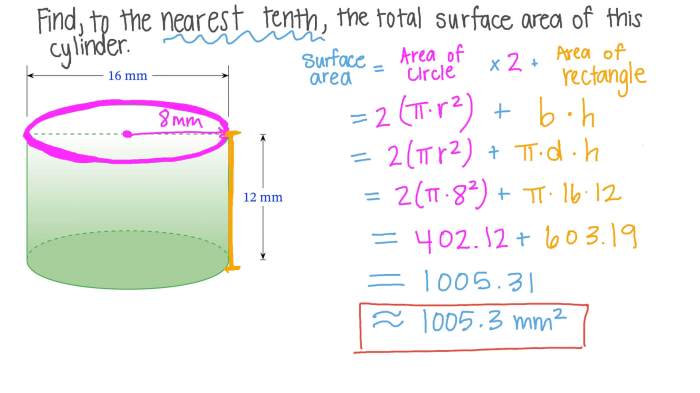
Contoh soal luas permukaan tabung merupakan topik penting dalam geometri. Memahami perhitungan luas permukaan tabung sangat krusial, karena berkaitan dengan berbagai aplikasi praktis dalam kehidupan sehari-hari. Dari menghitung kebutuhan cat untuk mengecat sebuah tangki penyimpanan hingga mendesain kemasan produk, kemampuan menghitung luas permukaan tabung menjadi keterampilan yang berharga. Mari kita telusuri rumus, contoh soal, dan penerapannya.
Artikel ini akan membahas secara rinci rumus luas permukaan tabung, menjelaskan langkah-langkah penyelesaian berbagai contoh soal dengan tingkat kesulitan berbeda, serta memberikan contoh penerapannya dalam kehidupan nyata. Dengan pemahaman yang komprehensif, Anda akan mampu menyelesaikan berbagai soal terkait luas permukaan tabung dengan mudah dan percaya diri.
Rumus Luas Permukaan Tabung
Menghitung luas permukaan tabung merupakan hal penting dalam berbagai aplikasi, mulai dari perencanaan konstruksi hingga desain kemasan produk. Memahami rumus dan penerapannya akan memudahkan kita dalam menyelesaikan berbagai permasalahan yang berkaitan dengan geometri tabung.
Luas permukaan tabung terdiri dari luas dua lingkaran alas dan luas selimut tabung. Rumus yang digunakan didapatkan dari penjumlahan luas-luas tersebut.
Rumus Luas Permukaan Tabung dan Penjelasan Variabel
Rumus luas permukaan tabung adalah:
L = 2πr² + 2πrh
di mana:
- L = Luas permukaan tabung
- r = Jari-jari alas tabung
- h = Tinggi tabung
- π (pi) ≈ 3,14
Istilah 2πr² mewakili luas kedua lingkaran alas tabung (masing-masing lingkaran memiliki luas πr²). Sementara itu, 2πrh merupakan luas selimut tabung, yang berbentuk persegi panjang dengan panjang sama dengan keliling alas tabung (2πr) dan lebar sama dengan tinggi tabung (h).
Penurunan Rumus Luas Permukaan Tabung
Rumus luas permukaan tabung diperoleh dengan menjumlahkan luas kedua lingkaran alas dan luas selimut tabung. Luas setiap lingkaran alas adalah πr², sehingga luas kedua lingkaran adalah 2πr². Luas selimut tabung merupakan perkalian keliling alas (2πr) dengan tinggi tabung (h), yaitu 2πrh. Oleh karena itu, total luas permukaan tabung adalah 2πr² + 2πrh.
Contoh Penerapan Rumus
Misalkan kita memiliki tabung dengan jari-jari r = 7 cm dan tinggi h = 10 cm. Maka luas permukaan tabung tersebut adalah:
L = 2π(7)² + 2π(7)(10) = 2π(49) + 140π = 98π + 140π = 238π cm² ≈ 747,7 cm²
Tabel Rumus Luas Permukaan Tabung, Contoh soal luas permukaan tabung
| Rumus | Variabel | Penjelasan | Satuan |
|---|---|---|---|
| L = 2πr² + 2πrh | L | Luas permukaan tabung | cm² atau satuan luas lainnya |
| r | Jari-jari alas tabung | cm atau satuan panjang lainnya | |
| h | Tinggi tabung | cm atau satuan panjang lainnya |
Ilustrasi Tabung
Bayangkan sebuah tabung tegak. Bagian bawah dan atas tabung merupakan lingkaran dengan jari-jari (r) yang sama. Jarak antara kedua lingkaran tersebut merupakan tinggi (h) tabung. Selimut tabung, jika dibentangkan, akan membentuk persegi panjang dengan panjang sama dengan keliling alas (2πr) dan lebar sama dengan tinggi tabung (h). Luas permukaan tabung didapat dari penjumlahan luas kedua lingkaran alas dan luas selimut tabung ini.
Contoh Soal Luas Permukaan Tabung dan Penyelesaiannya

Menghitung luas permukaan tabung merupakan aplikasi penting dari geometri dalam kehidupan sehari-hari. Kemampuan ini berguna dalam berbagai bidang, mulai dari perencanaan konstruksi hingga desain kemasan produk. Berikut ini disajikan beberapa contoh soal dengan tingkat kesulitan yang bervariasi, dilengkapi dengan penyelesaian langkah demi langkah.
Pemahaman yang baik tentang rumus luas permukaan tabung, yaitu 2πr(r+t) dimana ‘r’ adalah jari-jari alas dan ‘t’ adalah tinggi tabung, sangat krusial dalam menyelesaikan soal-soal ini. Rumus ini menggabungkan luas dua lingkaran alas dan luas selimut tabung.
Contoh Soal Luas Permukaan Tabung: Tingkat Kesulitan Mudah
Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan tabung tersebut.
Langkah 1: Identifikasi informasi yang diketahui. Jari-jari (r) = 7 cm, tinggi (t) = 10 cm.
Langkah 2: Gunakan rumus luas permukaan tabung: Luas Permukaan = 2πr(r + t)
Langkah 3: Substitusikan nilai r dan t ke dalam rumus: Luas Permukaan = 2 × π × 7 cm × (7 cm + 10 cm) = 2 × π × 7 cm × 17 cm = 238π cm² ≈ 747.7 cm²
Contoh Soal Luas Permukaan Tabung: Tingkat Kesulitan Sedang
Sebuah kaleng susu berbentuk tabung memiliki diameter 14 cm dan luas permukaan 1004.8 cm². Tentukan tinggi kaleng susu tersebut.
Langkah 1: Identifikasi informasi yang diketahui. Diameter = 14 cm, sehingga jari-jari (r) = 7 cm. Luas Permukaan = 1004.8 cm².
Langkah 2: Gunakan rumus luas permukaan tabung: Luas Permukaan = 2πr(r + t)
Langkah 3: Substitusikan nilai yang diketahui dan selesaikan persamaan untuk mencari t: 1004.8 cm² = 2 × π × 7 cm × (7 cm + t). Sederhanakan persamaan tersebut untuk mendapatkan nilai t. Setelah perhitungan, didapatkan t ≈ 15 cm.
Contoh Soal Luas Permukaan Tabung: Tingkat Kesulitan Sulit
Sebuah tangki air berbentuk tabung memiliki volume 770 cm³ dan tinggi 10 cm. Berapa luas permukaan tangki air tersebut?
Langkah 1: Hitung jari-jari (r) terlebih dahulu menggunakan rumus volume tabung: Volume = πr²t. 770 cm³ = πr² × 10 cm. Dari sini, kita bisa menghitung r ≈ 4.95 cm.
Langkah 2: Gunakan rumus luas permukaan tabung: Luas Permukaan = 2πr(r + t)
Langkah 3: Substitusikan nilai r dan t yang telah diketahui: Luas Permukaan = 2 × π × 4.95 cm × (4.95 cm + 10 cm) ≈ 469.2 cm²
Tabel Perbandingan Contoh Soal dan Penyelesaiannya
| No | Jari-jari (r) | Tinggi (t) | Luas Permukaan |
|---|---|---|---|
| 1 | 7 cm | 10 cm | ≈ 747.7 cm² |
| 2 | 7 cm | ≈ 15 cm | 1004.8 cm² |
| 3 | ≈ 4.95 cm | 10 cm | ≈ 469.2 cm² |
Penerapan Konsep Luas Permukaan Tabung dalam Kehidupan Sehari-hari
Konsep luas permukaan tabung, meskipun tampak sederhana dalam rumusnya, memiliki aplikasi yang luas dan penting dalam berbagai aspek kehidupan sehari-hari. Memahami luas permukaan tabung memungkinkan kita untuk mengoptimalkan penggunaan material, memperkirakan biaya produksi, dan bahkan memecahkan masalah praktis dalam berbagai industri.
Kaleng Minuman
Kaleng minuman, salah satu contoh paling umum dari tabung dalam kehidupan sehari-hari, dirancang dengan mempertimbangkan luas permukaannya. Produsen minuman selalu berupaya meminimalkan luas permukaan kaleng agar penggunaan bahan baku (logam) menjadi efisien dan biaya produksi dapat ditekan. Perhitungan luas permukaan membantu menentukan ukuran dan bentuk kaleng yang paling ekonomis tanpa mengorbankan kapasitas isi.
Ilustrasi: Bayangkan sebuah kaleng minuman soda. Luas permukaannya terdiri dari dua lingkaran (alas dan tutup) dan satu persegi panjang (selimut). Produsen minuman memperhitungkan luas permukaan total ini untuk menentukan jumlah logam yang dibutuhkan dalam pembuatan kaleng tersebut. Pengurangan luas permukaan secara efektif mengurangi penggunaan material dan biaya.
Poin Penting: Optimalisasi penggunaan material, pengurangan biaya produksi, efisiensi dalam proses manufaktur.
Pipa Saluran Air
Dalam sistem perpipaan, pemahaman tentang luas permukaan tabung sangat krusial. Luas permukaan pipa menentukan laju aliran air dan juga tingkat gesekan air dengan dinding pipa. Permukaan yang lebih luas dapat meningkatkan gesekan, mengurangi efisiensi aliran air, dan berpotensi menyebabkan penyumbatan. Oleh karena itu, pemilihan diameter pipa yang tepat berdasarkan perhitungan luas permukaan sangat penting untuk memastikan efisiensi sistem distribusi air.
Ilustrasi: Sebuah sistem irigasi pertanian menggunakan pipa-pipa dengan diameter tertentu. Luas permukaan dalam pipa ini mempengaruhi tekanan dan kecepatan aliran air yang dibutuhkan untuk mengairi lahan pertanian. Perhitungan yang tepat memastikan efisiensi penyiraman tanpa kehilangan tekanan yang signifikan.
Poin Penting: Efisiensi aliran, pengurangan gesekan, optimasi desain sistem perpipaan.
Kemasan Produk Silinder
Banyak produk dikemas dalam kemasan berbentuk silinder, seperti tabung pasta gigi, lilin, atau bahkan beberapa jenis makanan kaleng. Perhitungan luas permukaan tabung penting untuk menentukan jumlah material kemasan yang dibutuhkan dan juga untuk desain label produk. Desain label yang efektif membutuhkan perhitungan yang tepat agar label dapat menutupi seluruh permukaan tabung dengan sempurna.
Ilustrasi: Sebuah tabung pasta gigi. Luas permukaan tabung menentukan ukuran dan bentuk label yang dibutuhkan untuk menutupi seluruh permukaan tabung. Perhitungan yang tepat memastikan bahwa label terpasang dengan rapi dan informasi produk terlihat jelas.
Poin Penting: Desain kemasan yang efektif, optimalisasi penggunaan material kemasan, perencanaan desain label.
| Contoh Penerapan | Penjelasan Detail | Poin Penting |
|---|---|---|
| Kaleng Minuman | Minimisasi luas permukaan untuk efisiensi penggunaan material dan pengurangan biaya produksi. | Optimalisasi material, pengurangan biaya, efisiensi manufaktur. |
| Pipa Saluran Air | Pengaruh luas permukaan terhadap laju aliran air dan gesekan, pemilihan diameter pipa yang tepat. | Efisiensi aliran, pengurangan gesekan, optimasi desain sistem. |
| Kemasan Produk Silinder | Perhitungan luas permukaan untuk menentukan jumlah material kemasan dan desain label. | Desain kemasan efektif, optimalisasi material kemasan, perencanaan desain label. |
Soal Latihan Luas Permukaan Tabung: Contoh Soal Luas Permukaan Tabung
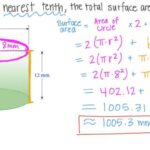
Setelah memahami rumus dan contoh perhitungan luas permukaan tabung, mari kita berlatih dengan beberapa soal. Soal-soal berikut ini dirancang untuk menguji pemahaman Anda terhadap konsep luas permukaan tabung dalam berbagai konteks. Perhatikan baik-baik setiap soal dan ikuti langkah-langkah penyelesaian yang telah dipelajari sebelumnya.
Soal Latihan Luas Permukaan Tabung dan Kunci Jawaban
Berikut lima soal latihan beserta kunci jawaban dan petunjuk tambahan untuk membantu Anda menyelesaikannya. Soal-soal ini memiliki tingkat kesulitan yang bervariasi, mulai dari yang sederhana hingga yang lebih kompleks, untuk mengasah kemampuan Anda.
| No. | Soal | Penyelesaian | Jawaban |
|---|---|---|---|
| 1 | Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitung luas permukaan tabung tersebut! | Luas permukaan tabung = 2πr(r + t) = 2 × 22/7 × 7 (7 + 10) = 748 cm² | 748 cm² |
| 2 | Tabung dengan diameter 14 cm dan tinggi 15 cm. Berapa luas permukaan tabung tersebut? Gunakan π = 22/7 | Jari-jari = 14/2 = 7 cm. Luas permukaan tabung = 2πr(r + t) = 2 × 22/7 × 7 (7 + 15) = 968 cm² | 968 cm² |
| 3 | Luas permukaan sebuah tabung adalah 1256 cm². Jika jari-jari alasnya 10 cm, tentukan tinggi tabung tersebut! (Gunakan π = 3,14) | 1256 = 2 × 3,14 × 10 (10 + t) ; 1256 = 62,8 (10 + t) ; 20 = 10 + t ; t = 10 cm | 10 cm |
| 4 | Sebuah kaleng berbentuk tabung memiliki tinggi 20 cm dan luas permukaan 1570 cm². Berapakah jari-jari alas kaleng tersebut? (Gunakan π = 3,14) | 1570 = 2 × 3,14 × r (r + 20) ; 250 = r² + 20r ; r² + 20r – 250 = 0 ; (r – 10)(r + 25) = 0 ; r = 10 cm (nilai negatif diabaikan) | 10 cm |
| 5 | Sebuah tangki air berbentuk tabung memiliki diameter 28 cm dan luas permukaan 3696 cm². Tentukan tinggi tangki air tersebut! (Gunakan π = 22/7) | Jari-jari = 28/2 = 14 cm. 3696 = 2 × 22/7 × 14 (14 + t) ; 3696 = 88 (14 + t) ; 42 = 14 + t ; t = 28 cm | 28 cm |
Petunjuk Tambahan dalam Menyelesaikan Soal Luas Permukaan Tabung
Ingatlah untuk selalu menuliskan rumus yang digunakan sebelum melakukan perhitungan. Pastikan satuan yang digunakan konsisten. Jika diberikan nilai π, gunakan nilai tersebut. Jika tidak, gunakan nilai pendekatan π = 3,14 atau π = 22/7 sesuai kebutuhan. Periksa kembali hasil perhitungan Anda untuk menghindari kesalahan.
Tips dan Trik: Pahami dengan baik rumus luas permukaan tabung, yaitu 2πr(r + t), di mana r adalah jari-jari alas dan t adalah tinggi tabung. Latihan rutin dan memahami konsep dasar geometri akan sangat membantu dalam menyelesaikan soal-soal luas permukaan tabung dengan cepat dan akurat. Jangan lupa untuk selalu memeriksa kembali jawaban Anda!
Pemungkas
Mempelajari luas permukaan tabung tidak hanya sekadar menghafal rumus, tetapi juga memahami konsep dan penerapannya. Dengan latihan yang cukup dan pemahaman yang mendalam, Anda akan mampu menyelesaikan berbagai permasalahan yang melibatkan perhitungan luas permukaan tabung. Semoga artikel ini memberikan pemahaman yang lebih baik dan membantu Anda dalam menguasai topik ini.