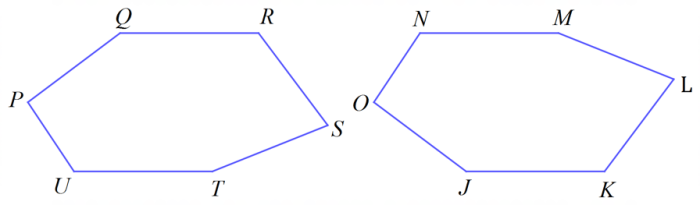
Pasangan bangun datar berikut ini pasti sebangun kecuali… Pertanyaan ini menggiring kita pada pemahaman mendalam tentang kesebangunan bangun datar. Konsep ini, yang tampak sederhana, ternyata memiliki aplikasi luas dalam berbagai bidang, mulai dari arsitektur hingga desain grafis. Memahami syarat dan ciri-ciri kesebangunan akan membantu kita mengidentifikasi pasangan bangun datar yang memang sebangun dan yang tidak.
Artikel ini akan membahas secara detail tentang kesebangunan bangun datar, meliputi definisi, syarat-syarat, identifikasi pasangan bangun datar yang tidak sebangun, serta penerapannya dalam kehidupan sehari-hari. Dengan contoh-contoh yang jelas dan ilustrasi yang mudah dipahami, diharapkan pemahaman Anda tentang konsep kesebangunan akan semakin mantap.
Kesebangunan Bangun Datar: Pasangan Bangun Datar Berikut Ini Pasti Sebangun Kecuali
Kesebangunan bangun datar merupakan konsep geometri yang penting dalam memahami hubungan antar bangun datar. Konsep ini menjelaskan bagaimana dua atau lebih bangun datar memiliki bentuk yang sama, meskipun ukurannya mungkin berbeda. Memahami kesebangunan sangat berguna dalam berbagai aplikasi, mulai dari desain arsitektur hingga pembuatan peta.
Definisi Kesebangunan Bangun Datar, Pasangan bangun datar berikut ini pasti sebangun kecuali
Dua bangun datar dikatakan sebangun jika sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar dan panjang sisi-sisi yang bersesuaian memiliki perbandingan yang tetap (sebanding). Artinya, bentuknya sama persis, hanya ukurannya yang mungkin berbeda. Perbandingan tetap ini disebut sebagai faktor skala.
Contoh Bangun Datar Sebangun
Perhatikan dua segitiga berikut. Segitiga A memiliki sisi dengan panjang 3 cm, 4 cm, dan 5 cm. Segitiga B memiliki sisi dengan panjang 6 cm, 8 cm, dan 10 cm. Kedua segitiga ini sebangun karena perbandingan sisi-sisi yang bersesuaian adalah tetap (6/3 = 8/4 = 10/5 = 2). Sudut-sudut yang bersesuaian juga sama besar.
Contoh Bangun Datar Tidak Sebangun
Sebuah persegi dengan sisi 5 cm dan sebuah persegi panjang dengan sisi 5 cm dan 7 cm tidak sebangun. Meskipun memiliki satu sisi yang sama panjang, perbandingan sisi-sisi yang bersesuaian tidak tetap. Selain itu, sudut-sudutnya pun tidak semuanya sama besar.
Perbandingan Ciri-ciri Bangun Datar Sebangun dan Tidak Sebangun
| Nama Bangun | Ciri-ciri | Sebangun/Tidak Sebangun | Alasan |
|---|---|---|---|
| Dua Segitiga | Sudut-sudut yang bersesuaian sama besar, perbandingan sisi-sisi yang bersesuaian tetap | Sebangun | Memenuhi definisi kesebangunan |
| Persegi dan Persegi Panjang | Sudut-sudut tidak semuanya sama besar, perbandingan sisi-sisi tidak tetap | Tidak Sebangun | Tidak memenuhi definisi kesebangunan |
| Dua Lingkaran | Bentuk sama, perbandingan jari-jari tetap | Sebangun | Memenuhi definisi kesebangunan |
| Segitiga Sama Sisi dan Segitiga Sama Kaki | Meskipun memiliki sudut yang sama, perbandingan sisi tidak selalu tetap | Tidak selalu sebangun | Tergantung pada panjang sisi-sisinya |
Ilustrasi Bangun Datar Sebangun dan Tidak Sebangun
Bayangkan dua segitiga sama sisi. Satu segitiga memiliki sisi 5 cm, dan yang lain memiliki sisi 10 cm. Kedua segitiga ini sebangun karena semua sudutnya 60 derajat, dan perbandingan sisi-sisi adalah 1:2. Sebagai kontras, bayangkan sebuah persegi dengan sisi 4 cm dan sebuah persegi panjang dengan sisi 4 cm dan 6 cm. Meskipun memiliki satu sisi yang sama, bentuknya berbeda, sudutnya berbeda (persegi memiliki 4 sudut 90 derajat, sedangkan persegi panjang juga memiliki 4 sudut 90 derajat, tetapi perbandingan sisinya tidak tetap), sehingga tidak sebangun.
Syarat-Syarat Kesebangunan Bangun Datar

Kesebangunan bangun datar merupakan konsep penting dalam geometri yang menjelaskan hubungan antara dua atau lebih bangun datar yang memiliki bentuk sama, meskipun ukurannya berbeda. Memahami syarat-syarat kesebangunan sangat krusial dalam berbagai aplikasi, mulai dari pembuatan peta hingga desain arsitektur. Artikel ini akan membahas syarat-syarat kesebangunan untuk beberapa bangun datar umum, yaitu segitiga, persegi panjang, dan persegi, serta membandingkan syarat-syarat tersebut.
Syarat Kesebangunan Segitiga
Terdapat beberapa syarat yang harus dipenuhi agar dua buah segitiga dinyatakan sebangun. Syarat-syarat ini memudahkan kita untuk menentukan kesebangunan tanpa harus mengukur semua sisi dan sudut.
- Kriteria Sudut-Sudut (SSS): Dua segitiga sebangun jika ketiga sudut yang bersesuaian pada kedua segitiga tersebut sama besar.
- Kriteria Sisi-Sisi-Sisi (SSS): Dua segitiga sebangun jika perbandingan panjang sisi-sisi yang bersesuaian pada kedua segitiga tersebut sama.
- Kriteria Sisi-Sudut-Sisi (SAS): Dua segitiga sebangun jika dua pasang sisi yang bersesuaian memiliki perbandingan yang sama dan sudut apit di antara kedua sisi tersebut sama besar.
Syarat Kesebangunan Persegi Panjang
Persegi panjang, sebagai bangun datar yang memiliki empat sudut siku-siku dan sisi-sisi yang berhadapan sama panjang, memiliki syarat kesebangunan yang lebih sederhana dibandingkan segitiga.
- Perbandingan Sisi yang Bersesuaian: Dua persegi panjang sebangun jika perbandingan panjang sisi-sisi yang bersesuaian adalah sama. Artinya, perbandingan panjang dan lebar pada persegi panjang pertama sama dengan perbandingan panjang dan lebar pada persegi panjang kedua.
Syarat Kesebangunan Persegi
Persegi, sebagai kasus khusus dari persegi panjang dengan semua sisi sama panjang, memiliki syarat kesebangunan yang sangat sederhana.
- Perbandingan Sisi: Dua persegi selalu sebangun, karena perbandingan sisi-sisi yang bersesuaian selalu sama, meskipun panjang sisinya berbeda.
Perbandingan Syarat Kesebangunan Segitiga dan Persegi Panjang
Berikut perbandingan syarat kesebangunan segitiga dan persegi panjang dalam bentuk poin-poin:
- Segitiga memiliki tiga kriteria kesebangunan (SSS, SAS, Sudut-Sudut), sementara persegi panjang hanya memiliki satu kriteria (perbandingan sisi yang bersesuaian).
- Syarat kesebangunan segitiga melibatkan sudut dan sisi, sedangkan persegi panjang hanya melibatkan sisi.
- Verifikasi kesebangunan segitiga bisa lebih kompleks karena melibatkan pengukuran sudut dan sisi, sedangkan persegi panjang lebih mudah diverifikasi karena hanya melibatkan perbandingan panjang sisi.
Contoh Bangun Datar Sebangun dan Tidak Sebangun
Berikut beberapa contoh untuk mengilustrasikan konsep kesebangunan:
- Sebangun: Dua peta Indonesia dengan skala berbeda. Meskipun ukurannya berbeda, kedua peta tersebut sebangun karena perbandingan panjang dan lebar pulau-pulau yang bersesuaian tetap konstan. Contoh lain adalah dua foto yang diambil dari sudut yang sama, tetapi dengan jarak fokus yang berbeda. Bentuk objek dalam foto tersebut akan tetap sebangun.
- Tidak Sebangun: Sebuah persegi dan sebuah lingkaran. Meskipun keduanya merupakan bangun datar, bentuknya berbeda sehingga tidak mungkin sebangun. Contoh lain adalah dua segitiga dengan sudut-sudut yang berbeda. Meskipun ukuran sisinya sama, karena sudutnya tidak sama, maka segitiga tersebut tidak sebangun.
Identifikasi Pasangan Bangun Datar yang Tidak Sebangun

Sebangun merupakan konsep penting dalam geometri yang menjelaskan kesamaan bentuk antara dua bangun datar. Dua bangun datar dikatakan sebangun jika sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Artikel ini akan membahas bagaimana mengidentifikasi pasangan bangun datar yang pasti tidak sebangun, disertai dengan contoh dan penjelasan detail.
Mengidentifikasi pasangan bangun datar yang tidak sebangun membutuhkan pemahaman yang mendalam tentang sifat-sifat bangun datar dan konsep kesebangunan. Perbedaan pada sudut atau perbandingan sisi yang tidak konsisten akan menunjukkan bahwa dua bangun datar tersebut tidak sebangun.
Contoh Pasangan Bangun Datar yang Tidak Sebangun
Berikut beberapa contoh pasangan bangun datar yang pasti tidak sebangun, beserta alasannya:
- Dua segitiga dengan sudut yang berbeda: Misalnya, segitiga pertama memiliki sudut 60°, 60°, dan 60° (segitiga sama sisi), sedangkan segitiga kedua memiliki sudut 30°, 60°, dan 90° (segitiga siku-siku). Karena sudut-sudut yang bersesuaian tidak sama besar, kedua segitiga ini tidak sebangun.
- Dua persegi panjang dengan perbandingan sisi yang tidak sama: Misalnya, persegi panjang pertama memiliki panjang 10 cm dan lebar 5 cm, sedangkan persegi panjang kedua memiliki panjang 12 cm dan lebar 6 cm. Meskipun perbandingan panjang dan lebar masing-masing persegi panjang sama (2:1), ukuran absolutnya berbeda. Walaupun keduanya memiliki sudut yang sama (semua sudut 90 derajat), perbandingan sisi-sisi yang bersesuaian tidak sama, sehingga tidak sebangun.
- Sebuah lingkaran dan sebuah segitiga: Lingkaran dan segitiga memiliki bentuk yang sangat berbeda. Tidak mungkin untuk menemukan sudut atau sisi yang bersesuaian dengan perbandingan yang sama antara kedua bangun ini. Oleh karena itu, mereka jelas tidak sebangun.
Ilustrasi Pasangan Bangun Datar yang Tidak Sebangun
Bayangkan sebuah persegi dengan sisi 4 cm dan sebuah persegi panjang dengan panjang 6 cm dan lebar 3 cm. Meskipun keduanya memiliki empat sudut siku-siku, perbandingan sisi-sisi yang bersesuaian tidak sama. Persegi memiliki perbandingan sisi 1:1, sementara persegi panjang memiliki perbandingan sisi 2:1. Perbedaan perbandingan sisi ini secara langsung menunjukkan bahwa kedua bangun datar tersebut tidak sebangun. Bentuk visualnya pun jelas berbeda, persegi tampak lebih ‘padat’ dibandingkan persegi panjang yang lebih memanjang.
Contoh Soal Cerita
Seorang arsitek merancang dua jendela dengan bentuk persegi panjang. Jendela pertama memiliki panjang 1,5 meter dan lebar 1 meter. Jendela kedua memiliki panjang 2 meter dan lebar 1,5 meter. Apakah kedua jendela tersebut sebangun?
Langkah-Langkah Penyelesaian Soal Cerita
- Identifikasi jenis bangun datar: Kedua jendela berbentuk persegi panjang.
- Bandingkan perbandingan sisi-sisi yang bersesuaian: Perbandingan panjang jendela pertama terhadap lebarnya adalah 1,5:1 atau 3:
2. Perbandingan panjang jendela kedua terhadap lebarnya adalah 2
1,5 atau 4:3. Perbandingan ini tidak sama.
- Kesimpulan: Karena perbandingan sisi-sisi yang bersesuaian tidak sama, kedua jendela tersebut tidak sebangun.
Ringkasan Identifikasi Pasangan Bangun Datar yang Tidak Sebangun
Untuk mengidentifikasi pasangan bangun datar yang tidak sebangun, periksa apakah sudut-sudut yang bersesuaian sama besar dan apakah perbandingan sisi-sisi yang bersesuaian sama. Jika salah satu kondisi ini tidak terpenuhi, maka kedua bangun datar tersebut tidak sebangun. Perbedaan bentuk visual yang signifikan juga dapat menjadi indikasi awal ketidaksebangun.
Penerapan Konsep Kesebangunan dalam Kehidupan Sehari-hari
Konsep kesebangunan bangun datar, meskipun tampak abstrak, memiliki aplikasi yang luas dan nyata dalam kehidupan sehari-hari. Memahami prinsip kesebangunan—yaitu perbandingan ukuran yang tetap antara bangun datar yang sebangun—memungkinkan kita untuk menyelesaikan berbagai masalah praktis, dari pembuatan peta hingga desain arsitektur.
Contoh Penerapan Kesebangunan: Peta
Peta merupakan representasi grafis dari suatu wilayah geografis. Peta dibuat dengan memperkecil ukuran wilayah sebenarnya, namun tetap mempertahankan proporsi dan bentuknya. Konsep kesebangunan diterapkan untuk memastikan bahwa jarak dan luas area pada peta berbanding lurus dengan jarak dan luas area sebenarnya di lapangan. Misalnya, jika skala peta adalah 1:100.000, maka setiap 1 cm pada peta mewakili 100.000 cm atau 1 km di lapangan.
Dengan demikian, perhitungan jarak dan luas wilayah dapat dilakukan dengan akurat berdasarkan skala peta yang telah ditentukan.
Contoh Penerapan Kesebangunan: Desain Bangunan
Dalam arsitektur dan desain bangunan, kesebangunan digunakan untuk memperbesar atau memperkecil model bangunan. Arsitek sering membuat model bangunan berskala kecil untuk memvisualisasikan desain sebelum pembangunan dimulai. Model ini harus sebangun dengan bangunan sebenarnya agar proporsi dan detailnya akurat. Kesebangunan juga penting dalam memastikan kesesuaian antara berbagai bagian bangunan, seperti jendela, pintu, dan dinding, sehingga menghasilkan struktur yang kokoh dan estetis.
Contoh Penerapan Kesebangunan: Pembuatan Fotocopy
Mesin fotokopi memanfaatkan prinsip kesebangunan untuk memperbesar atau memperkecil dokumen. Ketika kita ingin membuat fotokopi dengan ukuran yang berbeda dari aslinya, mesin fotokopi akan mempertahankan rasio aspek dokumen asli. Dengan kata lain, bentuk dan proporsi dokumen tetap sama meskipun ukurannya berubah. Hal ini memastikan bahwa fotokopi yang dihasilkan tetap terbaca dan proporsional.
Pentingnya Memahami Konsep Kesebangunan
Pemahaman yang mendalam tentang kesebangunan bangun datar sangat penting dalam berbagai aplikasi. Kemampuan untuk memperbesar atau memperkecil objek sambil mempertahankan proporsi dan bentuknya sangat krusial dalam berbagai bidang, mulai dari teknik sipil dan arsitektur hingga kartografi dan desain grafis. Dengan memahami prinsip-prinsip kesebangunan, kita dapat menyelesaikan masalah-masalah praktis dengan lebih akurat dan efisien.
| Contoh | Deskripsi Penerapan | Manfaat | Gambar Deskriptif |
|---|---|---|---|
| Peta | Representasi wilayah geografis dengan skala tertentu, mempertahankan proporsi dan bentuk. | Memudahkan navigasi dan perencanaan, analisis wilayah. | Sebuah peta dengan skala yang tertera, menunjukkan perbandingan jarak pada peta dengan jarak sebenarnya di lapangan. Detail peta menggambarkan berbagai fitur geografis seperti jalan, sungai, dan bangunan, semuanya diperkecil secara proporsional. |
| Model Bangunan | Model berskala kecil yang sebangun dengan bangunan sebenarnya, digunakan untuk visualisasi dan perencanaan. | Memungkinkan pengecekan desain dan proporsi sebelum pembangunan, membantu dalam perencanaan dan penganggaran. | Model bangunan berskala kecil yang menunjukkan detail seperti jendela, pintu, dan atap. Proporsi model mencerminkan proporsi bangunan sebenarnya. |
| Fotocopy | Mesin fotokopi memperbesar atau memperkecil dokumen sambil mempertahankan rasio aspek. | Memungkinkan reproduksi dokumen dalam berbagai ukuran, memudahkan distribusi dan penyimpanan dokumen. | Sebuah dokumen asli dan fotokopinya yang diperbesar, menunjukkan bahwa bentuk dan proporsi dokumen tetap sama meskipun ukurannya berbeda. |
“Memahami konsep kesebangunan bukan hanya sekadar pengetahuan matematika, tetapi juga kunci untuk memecahkan berbagai permasalahan praktis dalam kehidupan sehari-hari.”
Pemungkas
Kesimpulannya, mengidentifikasi pasangan bangun datar yang sebangun atau tidak sebangun membutuhkan pemahaman yang cermat terhadap definisi dan syarat-syarat kesebangunan. Kemampuan ini tidak hanya penting dalam konteks matematika, tetapi juga berguna dalam berbagai aplikasi praktis di kehidupan nyata. Dengan latihan dan pemahaman yang mendalam, kita dapat dengan mudah membedakan pasangan bangun datar yang sebangun dan yang tidak.