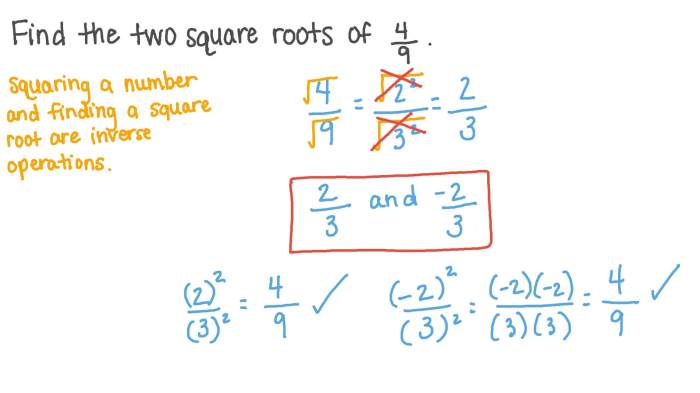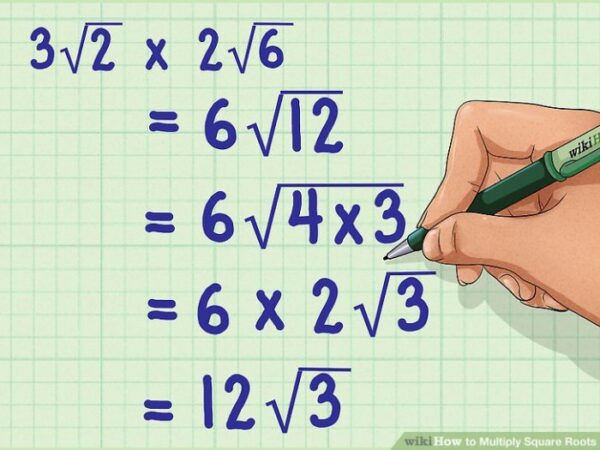8 akar 3, sebuah angka yang mungkin tampak sederhana namun menyimpan kekayaan konseptual dan aplikasi yang luas. Angka ini muncul dalam berbagai konteks matematika, geometri, dan bahkan ilmu terapan seperti fisika dan teknik. Dari representasi geometrisnya dalam segitiga siku-siku hingga perhitungan kompleks yang melibatkan operasi aljabar, 8 akar 3 menawarkan kesempatan untuk mendalami pemahaman kita tentang matematika dan aplikasinya di dunia nyata.
Artikel ini akan membahas secara komprehensif berbagai aspek dari 8 akar 3, mulai dari representasi geometrisnya hingga penerapannya dalam berbagai perhitungan dan pemecahan masalah. Kita akan menjelajahi cara menghitung dan memanipulasi angka ini, serta melihat contoh-contoh konkret bagaimana 8 akar 3 berperan dalam berbagai bidang.
Representasi Geometri “8 akar 3”
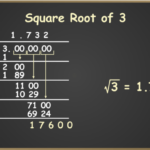
Nilai 8√3, meskipun tampak abstrak, dapat direpresentasikan secara geometrik dengan mudah, khususnya menggunakan segitiga siku-siku. Pemahaman representasi geometri ini penting karena memungkinkan visualisasi nilai tersebut dan menghubungkannya dengan konsep trigonometri dan vektor.
Segitiga Siku-Siku dan 8√3
Nilai 8√3 dapat divisualisasikan sebagai hipotenusa dari sebuah segitiga siku-siku. Misalnya, jika salah satu sisi tegaknya memiliki panjang 4 dan sisi tegak lainnya memiliki panjang 4√3, maka hipotenusanya akan memiliki panjang 8 (menggunakan teorema Pythagoras: 4² + (4√3)² = 16 + 48 = 64, √64 = 8). Dengan demikian, 8√3 dapat diinterpretasikan sebagai panjang hipotenusa dalam konteks segitiga siku-siku tertentu.
Ilustrasi segitiga siku-siku: Bayangkan segitiga siku-siku dengan sudut 30°, 60°, dan 90°. Sisi di depan sudut 30° berukuran 4, sisi di depan sudut 60° berukuran 4√3, dan hipotenusa berukuran 8. Perbandingan sisi-sisi ini menggambarkan hubungan antara nilai 8√3 dengan rasio trigonometri pada sudut 60°.
Representasi Geometri Alternatif 8√3
| Sisi A | Sisi B | Hipotenusa (8√3) | Sudut (derajat) |
|---|---|---|---|
| 4 | 4√3 | 8 | 30°, 60°, 90° |
| 8 | 8√3 | 16 | 30°, 60°, 90° |
| 2√6 | 6√2 | 8√3 | 45°, 45°, 90° |
| 4√3 | 4 | 8 | 60°, 30°, 90° |
Hubungan 8√3 dengan Nilai Trigonometri
Dalam segitiga siku-siku dengan sudut 30°, 60°, dan 90° yang telah dijelaskan sebelumnya, 8√3 mewakili hipotenusa. Nilai sinus 60° adalah (4√3)/8 = √3/2, cosinus 60° adalah 4/8 = 1/2, dan tangen 60° adalah (4√3)/4 = √3. Dengan demikian, 8√3 berkaitan erat dengan nilai-nilai trigonometri pada sudut 60°.
Diagram hubungan: Diagram akan menunjukkan segitiga siku-siku dengan sisi-sisi yang telah disebutkan, dan akan mencantumkan nilai sinus, cosinus, dan tangen dari sudut 60°, semuanya terkait dengan nilai 8√3 sebagai hipotenusa. Panjang sisi-sisi segitiga tersebut secara langsung berhubungan dengan perhitungan trigonometri untuk sudut 60°.
Representasi Vektor 8√3
Dalam ruang dua dimensi, 8√3 dapat direpresentasikan sebagai vektor. Misalnya, vektor dengan komponen (4, 4√3) memiliki besar (panjang) 8, yang merupakan nilai dari 8√3 dalam konteks ini. Ini berarti vektor tersebut mengarah ke titik (4, 4√3) pada bidang kartesian dan panjangnya adalah 8.
Sebagai contoh lain, vektor (8, 0) ditambah vektor (0, 8√3) akan menghasilkan vektor resultan dengan besar 8√3. Dengan demikian, berbagai kombinasi vektor dapat digunakan untuk mewakili nilai 8√3 secara geometrik.
Perhitungan dan Operasi Matematika Melibatkan “8 akar 3”

Akar 3 (√3) merupakan bilangan irasional, artinya memiliki nilai desimal yang tidak berulang dan tidak berakhir. Memahami operasi matematika yang melibatkan √3, termasuk 8√3, penting untuk menguasai aljabar dan kalkulus. Berikut ini akan dijelaskan beberapa perhitungan dan operasi matematika yang melibatkan 8√3, disertai contoh-contoh soal dan penyelesaiannya.
Penjumlahan dan Pengurangan Bilangan yang Mengandung √3
Penjumlahan dan pengurangan bilangan yang mengandung √3 dilakukan dengan cara menjumlahkan atau mengurangi koefisien dari √3, asalkan bentuk akarnya sama. Hal ini mirip dengan mengoperasikan variabel aljabar. Misalnya, untuk menjumlahkan atau mengurangi bilangan yang mengandung √3, kita hanya perlu memperhatikan koefisien dari √3.
- Contoh 1 (Penjumlahan): 8√3 + 5√3 = (8 + 5)√3 = 13√3
- Contoh 2 (Pengurangan): 12√3 – 8√3 = (12 – 8)√3 = 4√3
Perkalian Bilangan yang Mengandung √3
Perkalian bilangan yang mengandung √3 dilakukan dengan mengalikan koefisien dan akarnya secara terpisah. Ingatlah bahwa √3 x √3 = 3.
- Contoh: 8√3 x 2√3 = (8 x 2) x (√3 x √3) = 16 x 3 = 48
Contoh Soal Operasi Matematika yang Melibatkan 8√3
Berikut beberapa contoh soal yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian dengan bilangan yang mengandung √3, termasuk 8√3, beserta penyelesaiannya.
| No | Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|---|
| 1 | 8√3 + 5√3 – 2√3 | (8 + 5 – 2)√3 = 11√3 | 11√3 |
| 2 | 8√3 x 4 | 8 x 4 x √3 = 32√3 | 32√3 |
| 3 | 24√3 / 8√3 | (24/8) x (√3/√3) = 3 x 1 = 3 | 3 |
| 4 | (8√3)² | 8² x (√3)² = 64 x 3 = 192 | 192 |
Algoritma Sederhana untuk Menghitung Operasi Matematika yang Melibatkan 8√3
Algoritma sederhana untuk menghitung operasi matematika yang melibatkan 8√3 dan bilangan rasional lainnya dapat dirumuskan sebagai berikut:
- Pisahkan koefisien (bilangan rasional) dan √3.
- Lakukan operasi matematika (penjumlahan, pengurangan, perkalian, atau pembagian) pada koefisien.
- Jika operasi melibatkan perkalian √3 dengan √3, hasilkan 3.
- Gabungkan hasil operasi koefisien dengan √3 (jika ada).
- Sederhanakan hasil jika memungkinkan.
Penerapan “8 akar 3” dalam Konteks Tertentu
Nilai 8√3, meskipun tampak spesifik, muncul dalam berbagai perhitungan geometri dan aplikasi praktis di bidang teknik dan arsitektur. Keberadaannya seringkali berkaitan dengan sifat-sifat geometri bangun ruang tertentu, khususnya yang melibatkan segitiga sama sisi dan kubus.
Luas Segitiga Sama Sisi
Nilai 8√3 sering muncul dalam perhitungan luas segitiga sama sisi. Rumus luas segitiga sama sisi adalah (√3/4)s², dimana s adalah panjang sisi. Jika luas segitiga sama sisi adalah 8√3, maka kita dapat menghitung panjang sisinya. Berikut contohnya:
Contoh Soal: Sebuah segitiga sama sisi memiliki luas 8√3 satuan luas. Tentukan panjang sisi segitiga tersebut.
Penyelesaian:
- Rumus luas segitiga sama sisi: Luas = (√3/4)s²
- Substitusikan nilai luas: 8√3 = (√3/4)s²
- Sederhanakan persamaan: s² = (8√3 – 4) / √3 = 32
- Akar kuadrat kedua ruas: s = √32 = 4√2
Jadi, panjang sisi segitiga sama sisi tersebut adalah 4√2 satuan panjang.
Panjang Diagonal Kubus, 8 akar 3
Nilai 8√3 juga dapat ditemukan dalam perhitungan panjang diagonal ruang pada kubus. Diagonal ruang kubus menghubungkan dua titik sudut yang berseberangan. Panjang diagonal ruang kubus dengan panjang rusuk ‘a’ adalah a√3. Jika panjang diagonal ruang kubus adalah 8√3, kita dapat menentukan panjang rusuknya.
Ilustrasi: Bayangkan sebuah kubus. Diagonal ruangnya merupakan garis lurus yang menghubungkan suatu titik sudut ke titik sudut yang berlawanan, melewati bagian dalam kubus.
Contoh Perhitungan: Misalkan panjang diagonal ruang sebuah kubus adalah 8√3 cm. Maka panjang rusuknya (a) dapat dihitung sebagai berikut:
- Rumus diagonal ruang kubus: d = a√3
- Substitusikan nilai diagonal ruang: 8√3 = a√3
- Sederhanakan persamaan: a = 8
Jadi, panjang rusuk kubus tersebut adalah 8 cm.
Penerapan dalam Ilmu Fisika dan Teknik
Dalam beberapa kasus mekanika, terutama yang melibatkan struktur tiga dimensi, nilai 8√3 bisa muncul dalam perhitungan momen inersia atau tegangan pada struktur tertentu. Misalnya, dalam analisis struktur rangka baja, nilai ini bisa muncul saat menghitung gaya internal pada batang-batang yang membentuk sudut tertentu.
Penerapan dalam Geometri Ruang Tiga Dimensi
Selain kubus, nilai 8√3 bisa muncul dalam perhitungan volume dan luas permukaan berbagai bangun ruang lainnya. Misalnya, dalam tetrahedron beraturan (bangun ruang dengan empat sisi segitiga sama sisi), nilai ini bisa terkait dengan perhitungan jarak antar titik sudut atau volume.
Ilustrasi: Bayangkan sebuah tetrahedron beraturan. Jika kita menghitung jarak antara dua titik sudut yang berlawanan, dalam kondisi tertentu, perhitungan tersebut mungkin melibatkan nilai 8√3, tergantung pada panjang rusuk tetrahedron tersebut.
Penerapan dalam Arsitektur dan Konstruksi
Dalam desain bangunan, nilai 8√3 bisa muncul dalam perhitungan dimensi struktur atau penentuan posisi elemen-elemen bangunan. Misalnya, dalam perencanaan penempatan kolom penyangga pada atap berbentuk piramida atau struktur lainnya yang melibatkan segitiga sama sisi.
Contoh Kasus: Misalkan seorang arsitek merancang atap berbentuk piramida dengan alas persegi. Jika jarak antara dua titik sudut berlawanan pada alas piramida adalah 8√3 meter, dan atap tersebut berbentuk piramida segitiga sama sisi, maka perhitungan ketinggian piramida dan panjang sisi alas akan melibatkan nilai 8√3 dalam proses perhitungannya.
Approximation dan Nilai Desimal “8 akar 3”

Menentukan nilai desimal dari 8√3 secara tepat membutuhkan kalkulator atau perangkat lunak matematika. Namun, kita dapat melakukan pendekatan untuk memperoleh nilai hampiran yang cukup akurat untuk berbagai keperluan. Pemahaman tentang pendekatan ini penting, karena dalam banyak aplikasi praktis, nilai eksak tidak selalu dibutuhkan, dan pendekatan yang efisien lebih diutamakan.
Perhitungan Nilai Desimal 8√3
Untuk menghitung nilai desimal 8√3 hingga 4 angka di belakang koma, kita dapat menggunakan kalkulator. Akar kuadrat dari 3 (√3) kira-kira 1.7321. Oleh karena itu, 8√3 ≈ 8 x 1.7321 = 13.8568.
Perbandingan Nilai Pendekatan dengan Nilai Sebenarnya
Selisih antara nilai pendekatan dan nilai sebenarnya bergantung pada metode pendekatan dan jumlah angka desimal yang digunakan. Semakin banyak angka desimal yang digunakan, semakin kecil selisihnya. Sebagai contoh, jika kita menggunakan √3 ≈ 1.732, maka 8√3 ≈ 13.856. Selisihnya dengan nilai yang lebih akurat (13.8568) adalah 0.0008, yang relatif kecil untuk kebanyakan aplikasi.
Tabel Perbandingan Metode Pendekatan 8√3
Beberapa metode pendekatan dapat digunakan untuk menghitung 8√3, menghasilkan nilai hampiran yang berbeda tingkat akurasinya. Berikut tabel perbandingan beberapa metode tersebut:
| Metode Pendekatan | Nilai √3 | Nilai 8√3 | Selisih dengan Nilai Akurat (13.8568) |
|---|---|---|---|
| Kalkulator Sederhana | 1.732 | 13.856 | 0.0008 |
| Kalkulator Ilmiah | 1.73205 | 13.8564 | 0.0004 |
| Metode Newton-Raphson (iterasi 3) | 1.73205 | 13.8564 | 0.0004 |
| Pendekatan Linier | 1.73 | 13.84 | 0.0168 |
Contoh Penggunaan Pendekatan Nilai 8√3 dalam Perhitungan Praktis
Bayangkan kita sedang menghitung panjang diagonal sebuah persegi dengan sisi sepanjang 8 cm. Panjang diagonalnya adalah 8√2 cm. Jika kita perlu menghitung luas segitiga sama sisi yang terbentuk dari diagonal tersebut, kita akan memerlukan nilai 8√3. Dalam situasi seperti ini, pendekatan 13.86 cm sudah cukup akurat untuk kebanyakan keperluan praktis.
Akurasi yang Diperlukan dalam Pendekatan Nilai 8√3
Akurasi yang dibutuhkan dalam pendekatan nilai 8√3 sangat bergantung pada konteks penggunaannya. Untuk perhitungan rekayasa yang presisi, akurasi yang tinggi sangat penting. Sebaliknya, untuk perhitungan estimasi atau perencanaan awal, pendekatan yang lebih kasar mungkin sudah cukup memadai. Sebagai contoh, dalam perhitungan luas lahan, pendekatan dengan satu atau dua angka desimal mungkin sudah cukup akurat, sementara dalam perhitungan komponen elektronik, akurasi hingga beberapa angka di belakang koma mungkin diperlukan.
Kesimpulan Akhir
8 akar 3, meskipun tampak sederhana, merupakan angka yang kaya akan makna dan aplikasi. Pemahaman yang mendalam tentang angka ini memberikan landasan yang kuat untuk memecahkan berbagai masalah dalam matematika, geometri, dan ilmu terapan. Dengan menguasai konsep-konsep yang telah dibahas, kita dapat menangani berbagai perhitungan dan menganalisis masalah yang melibatkan 8 akar 3 dengan lebih efektif dan efisien.
Semoga pemahaman ini bermanfaat dalam perjalanan belajar dan penerapan matematika Anda.