Akar 175, sebuah angka yang mungkin tampak sederhana, menyimpan misteri matematika yang menarik untuk diungkap. Dari perhitungan manual hingga penerapannya dalam masalah nyata, eksplorasi akar 175 menawarkan perjalanan yang kaya akan konsep matematika, mulai dari bilangan irasional hingga metode numerik. Kita akan mengupas bagaimana menghitung akar 175 dengan berbagai cara, menyederhanakannya, dan melihat perannya dalam berbagai konteks, termasuk geometri dan fisika.
Artikel ini akan membahas berbagai metode perhitungan akar 175, mulai dari pendekatan manual yang sederhana hingga penggunaan kalkulator dan software. Selanjutnya, akan dijelaskan sifat akar 175 sebagai bilangan irasional dan bagaimana penyederhanaannya. Kita juga akan melihat penerapan praktis akar 175 dalam memecahkan masalah dunia nyata, serta mengkaji metode numerik untuk menghitungnya dengan tingkat akurasi yang tinggi.
Perkiraan Nilai Akar 175
Menentukan nilai akar kuadrat dari 175 dapat dilakukan dengan beberapa metode, mulai dari perhitungan manual hingga menggunakan kalkulator atau perangkat lunak. Perbedaan metode ini akan menghasilkan tingkat akurasi yang berbeda pula. Berikut ini akan diuraikan perhitungan akar 175 dengan beberapa metode dan perbandingannya.
Perhitungan Manual dengan Metode Iteratif (Metode Babilonia)
Metode iteratif, seperti metode Babilonia, merupakan pendekatan untuk menemukan akar kuadrat secara bertahap. Metode ini dimulai dengan sebuah tebakan awal, lalu secara berulang memperbaiki tebakan tersebut hingga mencapai tingkat akurasi yang diinginkan. Berikut contoh perhitungan akar 175 menggunakan metode Babilonia:
- Tebakan awal: Misal kita ambil 13 (karena 13² = 169, yang dekat dengan 175).
- Iterasi pertama: (13 + 175/13) / 2 ≈ 13.2
- Iterasi kedua: (13.2 + 175/13.2) / 2 ≈ 13.228
- Iterasi ketiga: (13.228 + 175/13.228) / 2 ≈ 13.228756
Proses ini dapat dilanjutkan hingga mencapai tingkat akurasi yang diinginkan. Semakin banyak iterasi, semakin akurat hasilnya. Namun, perlu diingat bahwa metode ini bersifat pendekatan dan hasilnya tidak akan persis sama dengan nilai sebenarnya.
Perkiraan Nilai Akar 175 dengan Kalkulator Sederhana
Menggunakan kalkulator sederhana, kita dapat langsung mendapatkan nilai akar 175. Hasilnya akan lebih akurat dibandingkan dengan perhitungan manual karena kalkulator menggunakan algoritma yang lebih canggih.
Hasil perhitungan menggunakan kalkulator sederhana umumnya menunjukkan nilai sekitar 13.228756555323.
Perbandingan Hasil Perhitungan Manual dan Kalkulator Sederhana
Perbandingan hasil perhitungan manual (dengan metode iteratif) dan kalkulator sederhana menunjukkan perbedaan yang kecil, terutama setelah beberapa iterasi dalam metode manual. Perbedaan ini disebabkan oleh keterbatasan akurasi dalam perhitungan manual dan jumlah iterasi yang dilakukan. Kalkulator memiliki kemampuan komputasi yang lebih tinggi dan algoritma yang lebih efisien untuk menghasilkan nilai yang lebih akurat.
Rentang Nilai Akar 175
Akar 175 terletak di antara dua bilangan bulat berurutan, yaitu 13 dan 14. Hal ini karena 13² = 169 dan 14² = 196, dan 175 berada di antara kedua kuadrat tersebut.
Tabel Perbandingan Hasil Perhitungan Akar 175
| Metode | Langkah Perhitungan | Hasil | Keterangan |
|---|---|---|---|
| Metode Iteratif (Babilonia) – 3 Iterasi | Lihat penjelasan di atas | ≈ 13.228756 | Akurasi meningkat dengan jumlah iterasi |
| Kalkulator Sederhana | Input langsung ke kalkulator | ≈ 13.228756555323 | Hasil yang lebih akurat |
| Software Matematika (Contoh: MATLAB, Python) | Fungsi akar kuadrat bawaan | ≈ 13.228756555323 | Tingkat akurasi tinggi, bergantung pada presisi komputasi software |
Akar 175 dalam Konteks Matematika
Angka 175, sekilas tampak sederhana, namun menyimpan keunikan dalam representasi akarnya. Akar kuadrat dari 175 bukanlah bilangan bulat, melainkan termasuk dalam kategori bilangan irasional. Pemahaman tentang sifat irasional ini, serta kemampuan menyederhanakan bentuk akarnya, merupakan aspek penting dalam aljabar.
Akar 175, ditulis sebagai √175, dapat disederhanakan untuk memperoleh bentuk yang lebih ringkas dan mudah dipahami. Proses penyederhanaan ini melibatkan penguraian bilangan 175 menjadi faktor-faktor primanya, yang kemudian digunakan untuk menyederhanakan bentuk akar.
Penyederhanaan Akar 175
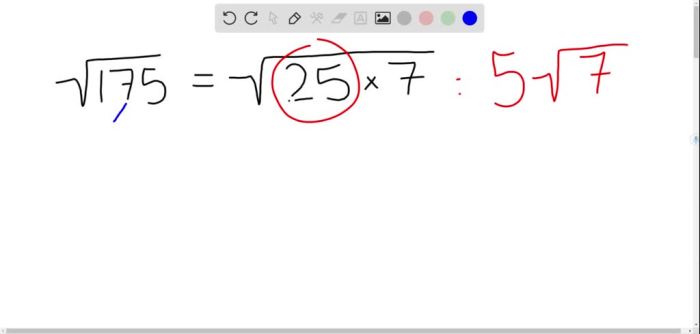
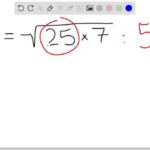
Untuk menyederhanakan √175, kita perlu mencari faktor-faktor prima dari 175. Melalui faktorisasi prima, kita temukan bahwa 175 = 5 x 5 x 7 = 5² x 7. Dengan demikian, √175 dapat ditulis sebagai √(5² x 7). Karena √(a x b) = √a x √b, maka √(5² x 7) = √5² x √7 = 5√7. Jadi, bentuk sederhana dari √175 adalah 5√7.
Faktor Prima 175 dan Hubungannya dengan Penyederhanaan
Faktorisasi prima 175 menjadi 5 x 5 x 7 (atau 5² x 7) merupakan kunci dalam penyederhanaan akarnya. Kehadiran faktor kuadrat (5²) memungkinkan kita untuk mengeluarkan angka 5 dari dalam tanda akar, sehingga menghasilkan bentuk yang lebih sederhana, yaitu 5√7. Jika tidak ada faktor kuadrat, maka akar tersebut sudah dalam bentuk paling sederhana.
Contoh Soal Matematika yang Melibatkan Akar 175
Misalkan kita memiliki persamaan: x² = 175. Untuk mencari nilai x, kita perlu menghitung akar kuadrat dari 175. Berdasarkan penyederhanaan sebelumnya, kita tahu bahwa √175 = 5√7. Oleh karena itu, solusi dari persamaan x² = 175 adalah x = ±5√7.
Letak Akar 175 pada Garis Bilangan Riil
Karena √175 ≈ 13.23 (nilai perkiraan), maka akar 175 terletak pada garis bilangan riil di antara bilangan bulat 13 dan 14. Lebih tepatnya, letaknya lebih dekat ke 13 karena 13.23 lebih dekat ke 13 daripada ke 14. Visualisasinya adalah sebuah titik pada garis bilangan yang berada di antara 13 dan 14, sedikit lebih mendekati 13. Kita dapat membayangkan jarak antara 13 dan 13.23 lebih pendek daripada jarak antara 13.23 dan 14.
Penerapan Akar 175 dalam Masalah Konkret

Akar 175, meskipun bukan angka bulat, memiliki aplikasi praktis dalam berbagai permasalahan, terutama dalam bidang geometri dan fisika. Pemahaman tentang perhitungan dan penerapan akar kuadrat ini penting untuk menyelesaikan masalah yang melibatkan panjang diagonal, luas, atau volume bangun ruang.
Menghitung Panjang Diagonal Persegi Panjang
Bayangkan sebuah taman berbentuk persegi panjang dengan panjang 10 meter dan lebar 7 meter. Kita ingin mengetahui panjang diagonal taman tersebut. Untuk menghitungnya, kita dapat menggunakan Teorema Pythagoras. Panjang diagonal (d) dapat dihitung dengan rumus: d = √(panjang² + lebar²).
Dalam kasus taman ini, panjang diagonalnya adalah:
d = √(10² + 7²) = √(100 + 49) = √149 ≈ 12.21 meter
Meskipun tidak secara langsung melibatkan akar 175, contoh ini menggambarkan bagaimana akar kuadrat digunakan dalam perhitungan geometri. Konsep yang sama dapat diterapkan pada situasi yang melibatkan akar 175.
Menghitung Sisi Segitiga Siku-Siku
Perhatikan segitiga siku-siku dengan hipotenusa sepanjang 175 cm. Jika salah satu sisi tegak lurusnya memiliki panjang 100 cm, kita dapat menghitung panjang sisi tegak lurus lainnya (a) menggunakan Teorema Pythagoras:
a² + 100² = 175²
a² = 175²
-100² = 30625 – 10000 = 20625
a = √20625 ≈ 143.6 cm
Contoh ini menunjukkan penerapan akar kuadrat dalam menghitung sisi segitiga siku-siku. Angka 175 berperan sebagai hipotenusa, dan perhitungannya melibatkan pengurangan kuadrat dan pengambilan akar kuadrat.
Menghitung Luas Segitiga
Misalkan kita memiliki segitiga dengan alas sepanjang 20 cm dan tinggi sepanjang 17.5 cm. Luas segitiga dapat dihitung dengan rumus:
Luas = ½
- alas
- tinggi
Substitusikan nilai yang diketahui:
Luas = ½
- 20 cm
- 17.5 cm = 175 cm²
Dalam contoh ini, angka 175 muncul secara langsung sebagai hasil perhitungan luas segitiga. Meskipun bukan akar 175 yang digunakan secara langsung, angka ini tetap relevan dalam konteks perhitungan geometri dan penggunaan angka desimal.
Pendekatan Numerik Akar 175
Menghitung akar kuadrat dari 175 secara tepat menggunakan metode manual cukup rumit. Oleh karena itu, pendekatan numerik menawarkan solusi yang efisien dan akurat. Beberapa metode numerik dapat digunakan untuk menghitung akar 175 dengan tingkat akurasi yang tinggi. Berikut ini akan dibahas beberapa metode tersebut, beserta perbandingan keefektifannya dan contoh implementasi salah satunya.
Metode Numerik untuk Menghitung Akar 175
Beberapa metode numerik yang umum digunakan untuk menghitung akar kuadrat, antara lain metode Newton-Raphson, metode Babilonia (atau metode Heron), dan metode biseksi. Ketiga metode ini memiliki prinsip kerja yang berbeda, sehingga menghasilkan efisiensi dan kecepatan konvergensi yang berbeda pula.
Perbandingan Keefektifan Metode Numerik
Metode Newton-Raphson umumnya dikenal sebagai metode yang paling efisien karena konvergensinya yang cepat, terutama jika nilai tebakan awal sudah cukup mendekati akar sebenarnya. Metode Babilonia, meskipun lebih sederhana, juga relatif efisien. Metode biseksi, meskipun konvergensinya lebih lambat, memiliki keunggulan dalam hal kestabilan dan jaminan konvergensi, asalkan interval awal dipilih dengan tepat.
Metode Numerik yang Paling Efisien untuk Akar 175
Untuk menghitung akar 175, metode Newton-Raphson umumnya dianggap paling efisien karena kecepatan konvergensinya. Metode ini iteratif, dan setiap iterasi menghasilkan pendekatan yang semakin mendekati akar sebenarnya dengan cepat.
Implementasi Metode Newton-Raphson untuk Akar 175
Metode Newton-Raphson menggunakan rumus iterasi: xn+1 = x n, di mana
-f(x n) / f'(x n) f(x) = x2 dan
-175 f'(x) = 2x. Misalkan kita mulai dengan tebakan awal x0 = 13 (karena 13 2 = 169, mendekati 175). Berikut langkah-langkah perhitungan:
x1 = 13 - (13 2- 175) / (2
- 13) ≈ 13.23
x2 = 13.23 - (13.23 2- 175) / (2
- 13.23) ≈ 13.22875656
x3 = 13.22875656 - (13.22875656 2- 175) / (2
- 13.22875656) ≈ 13.22875655532
Setelah beberapa iterasi, nilai akan konvergen ke akar 175, yaitu sekitar 13.22875655532.
Grafik Konvergensi Metode Newton-Raphson
Grafik konvergensi akan menunjukkan penurunan nilai selisih antara iterasi berturut-turut. Sumbu X mewakili nomor iterasi, dan sumbu Y mewakili nilai absolut selisih antara xn+1 dan xn. Grafik akan menunjukkan kurva yang menurun secara eksponensial, mendekati nol seiring dengan meningkatnya jumlah iterasi. Ini menunjukkan konvergensi yang cepat dari metode Newton-Raphson menuju akar 175. Kurva akan menunjukkan penurunan yang signifikan pada iterasi awal, kemudian penurunan yang lebih lambat seiring pendekatan ke nilai akar yang sebenarnya.
Nilai pada sumbu Y akan mendekati nol, menunjukkan bahwa perbedaan antara iterasi berturut-turut menjadi sangat kecil, menandakan konvergensi.
Pemungkas
Melalui eksplorasi ini, kita telah melihat bahwa akar 175, meskipun tampak sederhana, memiliki kedalaman matematis yang signifikan. Dari perhitungan manual hingga penerapannya dalam masalah geometri dan fisika, akar 175 menunjukkan keindahan dan kekuatan matematika dalam menyelesaikan berbagai permasalahan. Memahami akar 175 tidak hanya memperluas pengetahuan kita tentang matematika, tetapi juga menunjukkan bagaimana konsep matematika dasar dapat diterapkan untuk menyelesaikan masalah kompleks di dunia nyata.