Akar 5 adalah, dalam dunia matematika, sebuah bilangan irasional yang menarik dan memiliki banyak aplikasi. Bukan hanya sekadar angka, akar 5 merupakan kunci untuk memahami konsep-konsep geometri, aljabar, dan bahkan memiliki peran dalam aplikasi praktis kehidupan sehari-hari. Mari kita telusuri lebih dalam tentang representasi, perhitungan, dan pentingnya akar 5 dalam berbagai konteks.
Bilangan ini, yang secara desimal memiliki nilai tak hingga dan tak berulang, sering muncul dalam perhitungan geometri, khususnya dalam menentukan panjang diagonal persegi dan segitiga siku-siku. Pemahaman mendalam tentang akar 5 akan membuka pintu untuk memahami konsep matematika yang lebih kompleks dan aplikasinya dalam berbagai bidang ilmu pengetahuan dan teknologi.
Representasi Akar 5
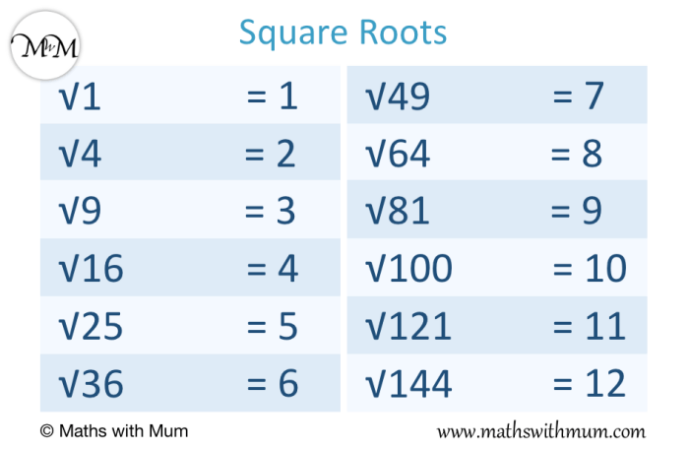
Akar 5, dinotasikan sebagai √5, merupakan bilangan irasional yang sering muncul dalam berbagai perhitungan matematika dan geometri. Bilangan ini tidak dapat dinyatakan sebagai pecahan sederhana dan memiliki nilai desimal yang tidak berulang. Berikut ini akan dijelaskan beberapa representasi akar 5.
Representasi Desimal Akar 5
Akar 5 dalam bentuk desimal, dengan 10 angka di belakang koma, adalah 2.2360679775. Nilai ini merupakan aproksimasi, karena akar 5 memiliki angka desimal yang tak terhingga dan tidak berulang.
Representasi Geometri Akar 5
Akar 5 dapat direpresentasikan secara geometri menggunakan segitiga siku-siku. Perhatikan segitiga siku-siku dengan panjang sisi tegak 1 dan 2. Dengan menggunakan teorema Pythagoras (a² + b² = c²), panjang sisi miring segitiga tersebut akan sama dengan √(1² + 2²) = √5. Jadi, panjang sisi miring segitiga siku-siku dengan sisi tegak 1 dan 2 adalah akar 5.
Perbandingan Akar 5 dengan Bilangan Bulat Terdekat
Tabel berikut menunjukkan perbandingan akar 5 dengan beberapa bilangan bulat terdekat, beserta selisihnya:
| Bilangan Bulat | Nilai | Akar 5 (≈2.236) | Selisih |
|---|---|---|---|
| 2 | 2 | 2.236 | 0.236 |
| 3 | 3 | 2.236 | 0.764 |
Perbandingan Akar 5 dengan Akar Kuadrat Lainnya
Akar 5 berada di antara akar 4 (yang sama dengan 2) dan akar 9 (yang sama dengan 3). Akar 4 dan akar 9 merupakan bilangan rasional, sedangkan akar 5 adalah bilangan irasional. Perbedaan utama terletak pada kemampuan untuk menyatakan bilangan tersebut sebagai pecahan sederhana. Akar 4 dan akar 9 dapat dinyatakan sebagai 2/1 dan 3/1, sedangkan akar 5 tidak dapat.
Contoh Penggunaan Akar 5 dalam Matematika Sederhana
Akar 5 dapat digunakan untuk menghitung panjang diagonal sebuah persegi dengan panjang sisi 1. Dengan menggunakan teorema Pythagoras, panjang diagonalnya adalah √(1² + 1²) = √2. Jika panjang sisi persegi adalah 2, maka panjang diagonalnya adalah √(2² + 2²) = √8 = 2√2. Namun, jika kita memiliki persegi panjang dengan sisi 2 dan 1, maka panjang diagonalnya adalah √(2² + 1²) = √5.
Perhitungan dan Aproksimasi Akar 5: Akar 5 Adalah

Akar 5, atau √5, merupakan bilangan irasional, artinya tidak dapat dinyatakan sebagai pecahan sederhana. Oleh karena itu, perhitungannya memerlukan metode aproksimasi. Berikut ini akan dijelaskan beberapa metode perhitungan dan aproksimasi akar 5, beserta perbandingan akurasinya.
Metode Iterasi Newton-Raphson untuk Akar 5
Metode Newton-Raphson merupakan metode iteratif untuk mencari akar suatu fungsi. Untuk mencari akar 5, kita dapat menggunakan fungsi f(x) = x²
–
5. Rumus iterasinya adalah: x n+1 = x n
-f(x n) / f'(x n), dimana f'(x) adalah turunan pertama dari f(x). Dalam kasus ini, f'(x) = 2x.
- Iterasi 1: Misalkan x0 = 2. Maka x 1 = 2 – (2²
5) / (2*2) = 2 – (-1) / 4 = 2.25
- Iterasi 2: x 2 = 2.25 – (2.25² – 5) / (2*2.25) ≈ 2.23611
- Iterasi 3: x 3 = 2.23611 – (2.23611² – 5) / (2*2.23611) ≈ 2.23607
Setelah tiga iterasi, nilai pendekatan akar 5 adalah sekitar 2.23607.
Metode Babilonia untuk Akar 5
Metode Babilonia, juga dikenal sebagai metode Heron, merupakan metode iteratif yang lebih sederhana dibandingkan Newton-Raphson. Rumusnya adalah: x n+1 = (x n + 5/x n) / 2
- Iterasi 1: Misalkan x0 = 2. Maka x 1 = (2 + 5/2) / 2 = 2.25
- Iterasi 2: x 2 = (2.25 + 5/2.25) / 2 ≈ 2.23611
- Iterasi 3: x 3 = (2.23611 + 5/2.23611) / 2 ≈ 2.23607
Hasil pendekatan akar 5 setelah tiga iterasi dengan metode Babilonia juga sekitar 2.23607.
Metode Aproksimasi Akar 5
Berikut tiga metode aproksimasi akar 5 yang berbeda:
- Metode Pecahan Lanjutan: Akar 5 dapat didekati dengan pecahan lanjutan [2; 4, 4, 4, …]. Konvergensi pecahan ini memberikan pendekatan yang semakin akurat dengan penambahan suku. Contohnya, 2 + 1/4 = 2.25, 2 + 1/(4 + 1/4) ≈ 2.236.
- Metode Taylor Series: Dengan menggunakan deret Taylor untuk fungsi √(x+1) di sekitar x=4, kita dapat memperoleh pendekatan akar 5. Metode ini membutuhkan perhitungan turunan fungsi dan evaluasi pada titik tertentu.
- Metode Interpolasi: Dengan menggunakan data titik-titik yang diketahui disekitar akar 5, metode interpolasi seperti linear atau polinomial dapat digunakan untuk mengaproksimasi nilai akar 5. Akurasi bergantung pada data titik dan metode interpolasi yang digunakan.
Perbandingan Akurasi Metode Aproksimasi
- Metode Newton-Raphson dan Babilonia menunjukkan konvergensi yang cepat dan akurasi yang tinggi setelah beberapa iterasi. Keduanya memberikan hasil yang hampir identik dalam contoh ini.
- Metode pecahan lanjutan memberikan pendekatan yang cukup akurat, tetapi konvergensinya lebih lambat dibandingkan metode iteratif.
- Akurasi metode Taylor Series dan interpolasi bergantung pada tingkat ketelitian dan kompleksitas perhitungan yang dilakukan. Semakin banyak suku yang digunakan dalam deret Taylor atau semakin banyak titik data yang digunakan dalam interpolasi, semakin akurat hasilnya.
Contoh Soal dan Penyelesaian
Sebuah segitiga siku-siku memiliki sisi siku-siku sepanjang 2 cm dan 3 cm. Berapakah panjang hipotenusanya?
Penyelesaian: Dengan teorema Pythagoras, panjang hipotenusa (c) dapat dihitung dengan rumus c² = a² + b², dimana a dan b adalah panjang sisi siku-siku. Dalam kasus ini, a = 2 cm dan b = 3 cm. Maka c² = 2² + 3² = 13 cm². Oleh karena itu, panjang hipotenusa adalah c = √13 cm. Karena √13 = √(4+9) = √(2²+3²) kita dapat mengaproksimasi nilai ini dengan menggunakan nilai √5 yang telah dihitung sebelumnya.
Meskipun contoh ini tidak secara langsung menggunakan √5, prinsip aproksimasi nilai akar kuadrat yang digunakan serupa dan relevan dengan konteks pembahasan.
Akar 5 dalam Konteks yang Lebih Luas
Angka irasional √5, meskipun tidak sering muncul secara eksplisit dalam kehidupan sehari-hari seperti angka-angka bulat, memainkan peran penting dalam berbagai bidang ilmu pengetahuan dan teknologi. Pemahaman tentang akar 5 membuka pintu untuk menyelesaikan berbagai masalah matematika dan memahami fenomena alam yang lebih kompleks.
Akar 5 dalam Rumus Matematika dan Fisika
Akar 5 muncul dalam berbagai rumus matematika, terutama dalam geometri dan trigonometri. Misalnya, diagonal dari persegi panjang dengan sisi 1 dan 2 memiliki panjang √5, sesuai dengan teorema Pythagoras. Dalam geometri tiga dimensi, akar 5 juga muncul dalam perhitungan panjang diagonal ruang pada bangun-bangun tertentu. Di bidang fisika, akar 5 dapat ditemukan dalam beberapa persamaan yang menjelaskan gerakan osilasi atau gelombang, meskipun tidak selalu secara langsung tampak.
Peran Akar 5 dalam Ilmu Pengetahuan dan Teknologi, Akar 5 adalah
Meskipun tidak sepopuler konstanta seperti π (pi) atau e (bilangan Euler), akar 5 memiliki aplikasi dalam berbagai bidang. Dalam arsitektur, rasio emas (sekitar 1.618), yang berhubungan erat dengan akar 5, sering digunakan untuk menciptakan proporsi yang estetis dan harmonis. Dalam ilmu komputer, akar 5 dapat digunakan dalam algoritma tertentu untuk optimasi dan perhitungan. Dalam analisis data dan statistika, akar 5 mungkin muncul dalam perhitungan tertentu, meskipun biasanya tidak sebagai elemen utama.
Aplikasi Praktis Akar 5 dalam Kehidupan Sehari-hari
Aplikasi praktis akar 5 dalam kehidupan sehari-hari mungkin tidak langsung terlihat, namun tetap ada. Misalnya, dalam perencanaan konstruksi, perhitungan jarak diagonal bangunan atau struktur tertentu bisa melibatkan akar 5. Dalam desain grafis atau seni, proporsi yang didasarkan pada rasio emas (yang terkait dengan akar 5) dapat digunakan untuk menciptakan desain yang menarik secara visual. Meskipun tidak sejelas penggunaan angka-angka bulat, akar 5 tetap berperan dalam berbagai aspek kehidupan, meskipun terkadang secara tidak langsung.
Pentingnya Memahami Konsep Akar 5
Memahami konsep akar 5, dan akar kuadrat secara umum, penting untuk mengembangkan pemahaman yang lebih komprehensif tentang matematika dan ilmu pengetahuan. Kemampuan untuk menghitung dan bekerja dengan akar kuadrat adalah keterampilan dasar yang dibutuhkan dalam berbagai bidang studi dan profesi. Ini membuka jalan untuk memahami konsep-konsep yang lebih kompleks dan memecahkan masalah yang lebih menantang.
Skenario Perhitungan yang Melibatkan Akar 5
Bayangkan seorang arsitek merancang sebuah ruangan persegi panjang dengan panjang 2 meter dan lebar 1 meter. Untuk menentukan panjang diagonal ruangan tersebut, ia perlu menghitung √(2² + 1²) = √5 meter. Hasil perhitungan ini penting untuk menentukan panjang kabel atau pipa yang dibutuhkan untuk instalasi di ruangan tersebut, memastikan perencanaan yang akurat dan efisien.
Sifat-Sifat Akar 5
Akar 5, dinotasikan sebagai √5, merupakan bilangan irasional yang memiliki sifat-sifat aljabar unik dan peranan penting dalam berbagai bidang matematika. Pemahaman terhadap sifat-sifatnya krusial untuk manipulasi dan penyederhanaan persamaan matematika yang melibatkannya.
Operasi Aljabar pada Akar 5
Akar 5, seperti bilangan lainnya, dapat dikenai operasi aljabar dasar. Berikut beberapa contohnya:
- Penjumlahan dan Pengurangan: √5 + √5 = 2√5; 3√5 – √5 = 2√5. Operasi ini hanya dapat dilakukan pada suku-suku sejenis yang mengandung akar 5.
- Perkalian: √5 × √5 = 5; √5 × 2√5 = 10; (√5) 2 = 5. Perkalian akar 5 dengan dirinya sendiri menghasilkan nilai 5.
- Pembagian: √5 / √5 = 1; 10√5 / 2√5 = 5. Pembagian akar 5 dengan dirinya sendiri menghasilkan nilai 1.
Rasionalitas Akar 5
Akar 5 dikategorikan sebagai bilangan irasional. Bilangan irasional adalah bilangan yang tidak dapat dinyatakan sebagai pecahan a/b, di mana a dan b adalah bilangan bulat dan b ≠ 0. Tidak ada dua bilangan bulat yang jika dibagi akan menghasilkan tepat √5. Nilai desimal akar 5 (≈ 2.236) merupakan bilangan desimal yang tidak berulang dan tidak berakhir.
Penyederhanaan dan Manipulasi Akar 5 dalam Persamaan
Akar 5 sering muncul dalam persamaan matematika, khususnya persamaan kuadrat. Penyederhanaan ekspresi yang melibatkan akar 5 seringkali melibatkan manipulasi aljabar untuk menyederhanakan bentuknya atau mengisolasi variabel.
Contoh Soal Penyederhanaan Ekspresi
Sederhanakan ekspresi berikut: 3√5 + 2√5 – √20.
Penyelesaian:
- Sederhanakan √20. Karena 20 = 4 x 5, maka √20 = √(4 x 5) = 2√5.
- Substitusikan nilai √20 ke dalam ekspresi awal: 3√5 + 2√5 – 2√5.
- Gabungkan suku-suku sejenis: 3√5.
Jadi, penyederhanaan ekspresi 3√5 + 2√5 – √20 menghasilkan 3√5.
Penggunaan Akar 5 dalam Persamaan Kuadrat
Akar 5 sering muncul sebagai solusi dalam persamaan kuadrat. Misalnya, perhatikan persamaan kuadrat x²
-5 = 0. Dengan memindahkan konstanta ke ruas kanan dan mengambil akar kuadrat dari kedua ruas, kita peroleh x = ±√5. Jadi, akar-akar persamaan kuadrat ini adalah x = √5 dan x = -√5.
Ringkasan Akhir
Kesimpulannya, akar 5, meskipun tampak sederhana, memiliki peran yang signifikan dalam matematika dan aplikasinya. Dari representasi geometri hingga perhitungan yang rumit, pemahaman yang baik tentang bilangan irasional ini sangat penting. Mempelajari akar 5 bukan hanya tentang angka itu sendiri, melainkan tentang memahami konsep-konsep dasar matematika dan aplikasinya dalam dunia nyata, yang membuka jalan untuk eksplorasi lebih lanjut dalam bidang ilmu pengetahuan dan teknologi.