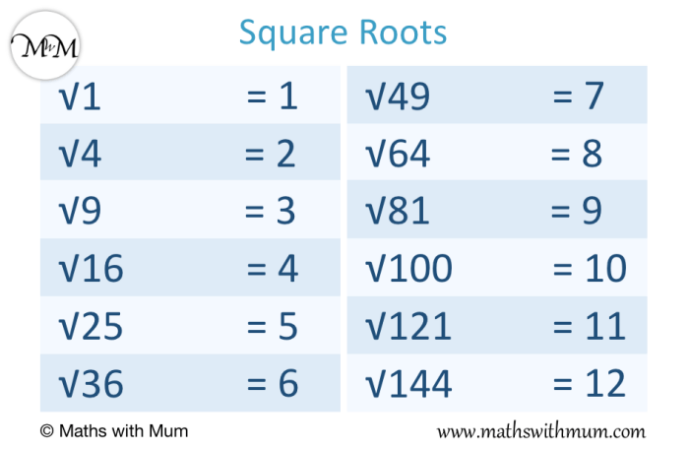
Akar dari 60, sebuah angka sederhana namun menyimpan misteri matematika yang menarik untuk diungkap. Perjalanan kita akan menelusuri berbagai aspek akar dari 60, mulai dari faktorisasi prima hingga representasi geometrisnya. Kita akan menghitung akar kuadrat dan akar kubik, serta mempelajari metode aproksimasi untuk mendapatkan nilai yang lebih akurat. Siapkan diri Anda untuk menjelajahi dunia angka yang penuh kejutan!
Pembahasan ini akan mencakup perhitungan langsung, perbandingan dengan akar angka terdekat, serta eksplorasi metode aproksimasi seperti metode iterasi Newton-Raphson. Selain itu, kita juga akan melihat representasi geometris akar 60, menghubungkannya dengan konsep luas bangun geometri dan teorema Pythagoras. Dengan pemahaman yang komprehensif, kita akan mengapresiasi keindahan dan kompleksitas matematika di balik angka sederhana ini.
Faktorisasi Prima dari 60
Angka 60, angka yang sering kita jumpai dalam kehidupan sehari-hari, menyimpan rahasia matematika yang menarik. Salah satunya adalah faktorisasi prima, sebuah proses penguraian angka menjadi perkalian bilangan prima. Memahami faktorisasi prima dari 60 akan membantu kita memahami sifat-sifat angka ini lebih dalam dan berguna dalam berbagai aplikasi matematika.
Faktor-faktor Prima dari 60
Faktor prima dari 60 adalah bilangan-bilangan prima yang jika dikalikan menghasilkan 60. Bilangan prima adalah bilangan bulat lebih besar dari 1 yang hanya habis dibagi 1 dan dirinya sendiri. Untuk menemukan faktor prima 60, kita dapat menggunakan metode pohon faktorisasi.
Pohon Faktorisasi Prima dari 60
Berikut ilustrasi pohon faktorisasi prima dari 60. Kita mulai dengan membagi 60 dengan bilangan prima terkecil, yaitu 2. Hasilnya 30, kemudian kita bagi lagi 30 dengan 2, hasilnya 15. Karena 15 bukan bilangan genap, kita bagi dengan bilangan prima berikutnya, yaitu 3. Hasilnya 5, yang merupakan bilangan prima.
Proses berhenti di sini. Jadi, faktorisasi prima dari 60 adalah 2 x 2 x 3 x 5 atau 2 2 x 3 x 5.
Bayangkan sebuah pohon terbalik. Di puncaknya terdapat angka 60. Kemudian cabang pertama berbuah 2 dan 30. Cabang 30 berbuah 2 dan 15. Cabang 15 berbuah 3 dan 5.
Angka 2, 3, dan 5 merupakan daun yang merupakan bilangan prima.
Tabel Faktorisasi Prima 60 dan Pangkatnya
Tabel berikut merangkum faktorisasi prima dari 60 dan pangkat masing-masing faktor prima:
| Faktor Prima | Pangkat |
|---|---|
| 2 | 2 |
| 3 | 1 |
| 5 | 1 |
Langkah-langkah Memperoleh Faktorisasi Prima dari 60
- Bagi 60 dengan bilangan prima terkecil, yaitu 2. Hasilnya 30.
- Bagi 30 dengan 2. Hasilnya 15.
- Karena 15 tidak habis dibagi 2, bagi 15 dengan bilangan prima berikutnya, yaitu 3. Hasilnya 5.
- 5 adalah bilangan prima, sehingga proses berhenti di sini.
- Faktorisasi prima dari 60 adalah 2 x 2 x 3 x 5, atau 22 x 3 x 5.
Semua Faktor dari 60
Setelah mengetahui faktorisasi prima, kita dapat menentukan semua faktor dari
60. Faktor adalah bilangan yang membagi habis 60 tanpa sisa. Dengan menggunakan faktorisasi prima (2 2 x 3 x 5), kita dapat menemukan semua kombinasi perkalian dari faktor-faktor prima tersebut:
- 1
- 2
- 3
- 4
- 5
- 6
- 10
- 12
- 15
- 20
- 30
- 60
Akar Kuadrat dari 60
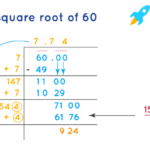
Akar kuadrat merupakan operasi matematika yang bertujuan untuk mencari bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) akan menghasilkan bilangan tertentu. Dalam konteks ini, kita akan membahas perhitungan akar kuadrat dari 60, membandingkannya dengan akar kuadrat angka terdekat, dan mengilustrasikan posisinya pada garis bilangan. Pemahaman tentang akar kuadrat sangat berguna dalam berbagai bidang, termasuk geometri, fisika, dan bahkan dalam perencanaan keuangan sehari-hari.
Perhitungan Akar Kuadrat 60
Akar kuadrat dari 60 dapat dihitung menggunakan kalkulator atau metode numerik. Hasilnya, dalam bentuk desimal dengan empat angka di belakang koma, adalah 7.7460. Perlu diingat bahwa akar kuadrat suatu bilangan selalu memiliki dua kemungkinan nilai, yaitu positif dan negatif. Namun, dalam konteks umum, kita seringkali hanya fokus pada akar kuadrat positif.
Perbandingan dengan Akar Kuadrat Angka Terdekat
Untuk lebih memahami posisi akar kuadrat 60, kita dapat membandingkannya dengan akar kuadrat angka-angka terdekat, yaitu 49 dan 64. Akar kuadrat dari 49 adalah 7, dan akar kuadrat dari 64 adalah 8. Oleh karena itu, akar kuadrat dari 60 (7.7460) terletak di antara 7 dan 8 pada garis bilangan.
Konsep Akar Kuadrat dan Cara Menghitungnya
Akar kuadrat dari suatu bilangan x, dinotasikan sebagai √ x, adalah bilangan yang jika dikuadratkan akan menghasilkan x. Dengan kata lain, √ x
– √ x = x. Ada beberapa metode untuk menghitung akar kuadrat, mulai dari metode perkiraan sederhana hingga penggunaan kalkulator atau perangkat lunak komputer. Metode perkiraan seringkali melibatkan pendekatan iteratif, mendekati nilai akar kuadrat secara bertahap.
Ilustrasi Akar Kuadrat 60 pada Garis Bilangan
Bayangkan sebuah garis bilangan. Tandai angka 7 dan 8 pada garis bilangan tersebut. Akar kuadrat dari 60, yaitu 7.7460, akan terletak di antara 7 dan 8, lebih dekat ke angka 8. Kita dapat membagi jarak antara 7 dan 8 menjadi sepuluh bagian yang sama. Kemudian, kita akan menemukan posisi 7.7460 yang berada sekitar ¾ jarak dari angka 7 menuju angka 8.
Visualisasi ini membantu kita memahami posisi akar kuadrat 60 secara relatif terhadap angka-angka terdekatnya.
Penerapan Akar Kuadrat dalam Kehidupan Sehari-hari
Akar kuadrat memiliki banyak aplikasi praktis. Misalnya, dalam geometri, akar kuadrat digunakan untuk menghitung panjang diagonal suatu persegi atau panjang sisi segitiga siku-siku menggunakan teorema Pythagoras ( a² + b² = c², di mana c adalah panjang sisi miring). Dalam fisika, akar kuadrat digunakan dalam berbagai rumus, seperti menghitung kecepatan atau energi. Bahkan dalam perencanaan keuangan, akar kuadrat dapat digunakan dalam perhitungan investasi atau analisis risiko.
Akar Kubik dari 60
Mencari akar kubik dari suatu angka berarti menemukan angka yang, jika dipangkatkan tiga, akan menghasilkan angka tersebut. Dalam kasus ini, kita akan menyelidiki akar kubik dari 60, membandingkannya dengan akar kubik angka-angka terdekat, dan menjelaskan perbedaan antara akar kuadrat dan akar kubik. Kita juga akan melihat contoh penerapan akar kubik dalam konteks geometri.
Perhitungan Akar Kubik dari 60
Akar kubik dari 60, ditulis sebagai ³√60, dapat dihitung menggunakan kalkulator atau melalui metode numerik iteratif. Hasilnya, dengan empat angka di belakang koma, adalah 3.9149.
Perbandingan dengan Akar Kubik Angka Terdekat
Mari bandingkan akar kubik 60 dengan akar kubik angka-angka terdekat, misalnya 64 dan 50. Akar kubik dari 64 adalah 4 (karena 4³ = 64), sedangkan akar kubik dari 27 adalah 3 (karena 3³=27). Perbedaan antara akar kubik 60 (3.9149) dan akar kubik 64 (4) relatif kecil, menunjukkan bahwa 60 relatif dekat dengan kubik sempurna 64. Perbedaan ini menunjukkan bagaimana nilai akar kubik berubah seiring perubahan angka pokoknya.
Perbedaan Akar Kuadrat dan Akar Kubik
Akar kuadrat dari suatu angka adalah angka yang, jika dikuadratkan (dikalikan dengan dirinya sendiri), akan menghasilkan angka tersebut. Akar kubik, seperti yang telah dijelaskan, adalah angka yang, jika dipangkatkan tiga (dikalikan dengan dirinya sendiri tiga kali), akan menghasilkan angka tersebut. Perbedaan mendasar terletak pada pangkat yang digunakan: dua untuk akar kuadrat dan tiga untuk akar kubik. Ini menghasilkan nilai yang berbeda untuk angka yang sama.
Sebagai contoh, akar kuadrat dari 64 adalah 8 (karena 8² = 64), sedangkan akar kubiknya adalah 4 (karena 4³ = 64).
Definisi Akar Kubik
Akar kubik dari suatu angka
- x* adalah angka
- y* sedemikian rupa sehingga
- y*³ =
- x*. Dengan kata lain, akar kubik adalah kebalikan dari operasi pemangkatan tiga.
Contoh Akar Kubik dalam Geometri
Bayangkan sebuah kubus dengan volume 60 cm³. Untuk mencari panjang rusuk kubus tersebut, kita perlu menghitung akar kubik dari volumenya. Panjang rusuk kubus tersebut adalah ³√60 cm ≈ 3.9149 cm. Ini menunjukkan bagaimana akar kubik digunakan untuk menyelesaikan masalah geometri yang melibatkan volume kubus atau bangun ruang lainnya yang memiliki bentuk kubus.
Aproksimasi Akar dari 60
Mencari akar kuadrat dari suatu bilangan tidak selalu menghasilkan bilangan bulat. Untuk bilangan seperti 60, kita perlu menggunakan metode aproksimasi. Metode iterasi Newton-Raphson merupakan salah satu teknik yang efektif untuk menghitung aproksimasi akar kuadrat dengan tingkat akurasi yang tinggi. Berikut akan dijelaskan langkah-langkah perhitungan dan perbandingannya dengan metode lain.
Aproksimasi Akar Kuadrat 60 dengan Metode Iterasi Newton-Raphson
Metode iterasi Newton-Raphson merupakan metode numerik untuk mencari akar dari suatu fungsi. Dalam konteks mencari akar kuadrat dari 60, kita dapat menggunakan fungsi f(x) = x²
–
60. Akar dari fungsi ini adalah akar kuadrat dari
60. Rumus iterasi Newton-Raphson adalah:
xn+1 = x n
f(xn) / f'(x n)
Dimana f'(x) adalah turunan pertama dari f(x). Dalam kasus ini, f'(x) = 2x. Dengan mengambil tebakan awal (x 0), misalnya 7, kita dapat melakukan iterasi hingga mencapai tingkat akurasi yang diinginkan. Berikut langkah-langkahnya:
- Iterasi 1: x1 = 7 – (7²
- 60) / (2
- 7) ≈ 7.714
- Iterasi 2: x 2 = 7.714 – (7.714²
- 60) / (2
- 7.714) ≈ 7.746
- Iterasi 3: x 3 = 7.746 – (7.746²
- 60) / (2
- 7.746) ≈ 7.746
Setelah iterasi ke-3, nilai sudah konvergen ke 7.746. Ini merupakan aproksimasi akar kuadrat dari 60 menggunakan metode Newton-Raphson.
Perbandingan Hasil Aproksimasi
Berikut tabel perbandingan hasil aproksimasi akar kuadrat 60 menggunakan beberapa metode. Nilai aktual akar kuadrat 60 berdasarkan kalkulator adalah sekitar 7.7459666924.
| Metode Aproksimasi | Iterasi ke- | Nilai Aproksimasi | Selisih dengan Nilai Aktual |
|---|---|---|---|
| Newton-Raphson | 3 | 7.746 | 0.0000333076 |
| Metode Babilonia (rata-rata tebakan dan 60/tebakan) | 3 | 7.746 | 0.0000333076 (Perkiraan, karena metode ini tidak memberikan nilai yang persis sama dengan Newton-Raphson pada iterasi yang sama) |
| Perkiraan sederhana (misal, antara 7 dan 8 karena 7²=49 dan 8²=64) | – | 7.75 | 0.0040333076 |
Kelebihan dan Kekurangan Metode Aproksimasi Akar Kuadrat
Berbagai metode aproksimasi akar kuadrat memiliki kelebihan dan kekurangan masing-masing. Metode Newton-Raphson, misalnya, dikenal karena konvergensinya yang cepat, tetapi membutuhkan perhitungan turunan fungsi. Metode Babilonia lebih sederhana secara perhitungan, namun mungkin membutuhkan lebih banyak iterasi untuk mencapai akurasi yang sama. Metode perkiraan sederhana mudah dihitung tetapi tingkat akurasinya rendah.
Algoritma Sederhana untuk Menghitung Aproksimasi Akar Kuadrat
Algoritma sederhana untuk menghitung aproksimasi akar kuadrat dapat diimplementasikan dengan metode Babilonia. Algoritma ini secara iteratif memperbaiki tebakan awal hingga mencapai tingkat akurasi yang diinginkan.
- Mulailah dengan tebakan awal x0.
- Hitung rata-rata antara x 0 dan n/x 0, dimana n adalah bilangan yang akar kuadratnya dicari.
- Gunakan hasil perhitungan sebagai tebakan baru (x 1).
- Ulangi langkah 2 dan 3 hingga selisih antara dua iterasi berturut-turut kurang dari toleransi yang ditentukan.
Representasi Geometris Akar dari 60
Akar kuadrat dari 60, dilambangkan sebagai √60, merupakan bilangan irasional yang tidak dapat dinyatakan sebagai pecahan sederhana. Namun, kita dapat merepresentasikannya secara geometris melalui beberapa pendekatan yang memanfaatkan konsep luas dan teorema Pythagoras. Representasi geometris ini membantu kita untuk memvisualisasikan nilai √60 dan hubungannya dengan bangun geometri.
Diagram Persegi Panjang
Salah satu cara untuk merepresentasikan √60 secara geometris adalah dengan menggunakan persegi panjang. Bayangkan sebuah persegi panjang dengan luas 60 satuan persegi. Jika salah satu sisinya memiliki panjang x, maka sisi lainnya akan memiliki panjang 60/x. Akar kuadrat dari 60 dapat divisualisasikan sebagai panjang sisi persegi yang memiliki luas yang sama dengan persegi panjang tersebut. Dengan mencoba berbagai nilai x, kita dapat mendekati nilai √60.
Misalnya, jika kita mengambil salah satu sisi persegi panjang sepanjang 7,5 satuan, sisi lainnya akan sepanjang 8 satuan (7,5 x 8 = 60). Persegi panjang ini mendekati sebuah persegi, yang panjang sisinya mendekati √60.
Hubungan Akar Kuadrat 60 dengan Luas Bangun Geometri, Akar dari 60
Ilustrasi yang menunjukkan hubungan antara akar kuadrat 60 dengan luas suatu bangun geometri dapat berupa sebuah persegi dengan luas 60 satuan persegi. Panjang sisi persegi ini akan sama dengan √60. Kita dapat membayangkan sebuah persegi dengan luas 60 cm², misalnya. Panjang setiap sisi persegi tersebut, yang merupakan akar kuadrat dari luasnya (√60 cm²), merepresentasikan nilai √60 secara visual.
Semakin akurat pengukuran luas persegi, semakin akurat pula representasi geometris dari √60.
Representasi Geometris Lain
Selain menggunakan persegi panjang dan persegi, akar kuadrat dari 60 juga dapat direpresentasikan dengan menggunakan segitiga siku-siku. Misalnya, dengan menerapkan teorema Pythagoras, kita dapat membuat segitiga siku-siku dengan panjang sisi a dan b, dimana a² + b² = 60. Hipotenusa segitiga ini (sisi miring) akan memiliki panjang √60. Berbagai kombinasi nilai a dan b dapat digunakan untuk menghasilkan segitiga siku-siku dengan hipotenusa yang merepresentasikan √60.
Contohnya, jika a = 2 dan b = √56 (karena 2² + √56² = 4 + 56 = 60), maka hipotenusa segitiga ini akan berpanjang √60.
Hubungan Akar Kuadrat dan Teorema Pythagoras
Teorema Pythagoras, a² + b² = c², memiliki hubungan erat dengan representasi geometris akar kuadrat. Dalam konteks √60, kita dapat memilih nilai a dan b sedemikian rupa sehingga jumlah kuadratnya sama dengan 60. Maka, panjang hipotenusa (c) dari segitiga siku-siku tersebut akan sama dengan √60. Ini menunjukkan bahwa akar kuadrat suatu bilangan dapat diinterpretasikan sebagai panjang hipotenusa segitiga siku-siku dengan sisi-sisi yang memenuhi teorema Pythagoras.
Penutupan Akhir
Melalui eksplorasi akar dari 60, kita telah menyaksikan bagaimana konsep matematika dasar dapat diterapkan dan diinterpretasikan dalam berbagai cara. Dari faktorisasi prima hingga representasi geometris, setiap pendekatan memberikan wawasan yang unik tentang sifat angka tersebut. Semoga perjalanan ini telah memperkaya pemahaman kita tentang matematika dan menunjukkan keindahan tersembunyi di balik angka-angka yang tampak sederhana.