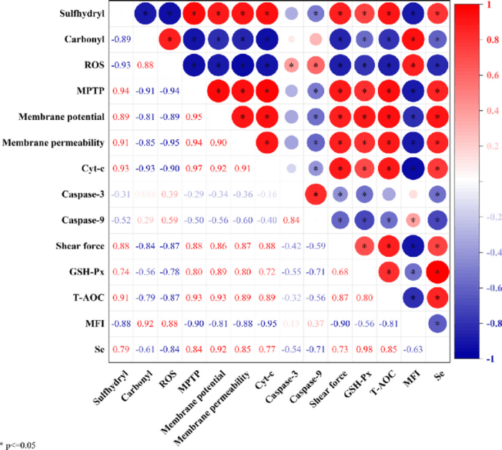
Analisis korelasi merupakan alat statistik yang ampuh untuk mengungkap hubungan antara dua atau lebih variabel. Bayangkan Anda ingin mengetahui apakah ada kaitan antara jumlah iklan yang ditayangkan dengan peningkatan penjualan produk. Atau mungkin Anda penasaran apakah ada korelasi antara tingkat pendidikan dengan pendapatan seseorang. Analisis korelasi dapat memberikan jawabannya, membantu kita memahami pola dan tren dalam data, serta membuat prediksi yang lebih akurat.
Metode ini melibatkan berbagai teknik, mulai dari korelasi Pearson yang umum digunakan untuk data numerik, hingga korelasi Spearman yang cocok untuk data ordinal. Kita akan menjelajahi berbagai jenis analisis korelasi, kekuatan dan kelemahan masing-masing, serta bagaimana menginterpretasikan hasilnya dengan tepat. Dengan pemahaman yang mendalam tentang analisis korelasi, kita dapat mengambil keputusan yang lebih baik berdasarkan data yang ada.
Pengantar Analisis Korelasi
Analisis korelasi merupakan metode statistik yang digunakan untuk mengukur kekuatan dan arah hubungan antara dua variabel atau lebih. Tujuan utama analisis ini adalah untuk menentukan seberapa kuat perubahan pada satu variabel dikaitkan dengan perubahan pada variabel lainnya, tanpa mengimplikasikan adanya hubungan sebab-akibat. Dengan kata lain, analisis korelasi membantu kita memahami pola hubungan antara data, bukan menjelaskan mengapa hubungan tersebut terjadi.
Penerapan analisis korelasi sangat luas, mencakup berbagai bidang seperti ekonomi, kesehatan, ilmu sosial, dan teknik. Misalnya, dalam ekonomi, korelasi dapat digunakan untuk menganalisis hubungan antara inflasi dan pengangguran. Di bidang kesehatan, korelasi dapat digunakan untuk mempelajari hubungan antara gaya hidup dan risiko penyakit jantung. Dalam ilmu sosial, korelasi dapat digunakan untuk mengkaji hubungan antara tingkat pendidikan dan pendapatan.
Jenis-jenis Analisis Korelasi
Beberapa jenis analisis korelasi yang umum digunakan meliputi korelasi Pearson, korelasi Spearman, dan korelasi Kendall. Pemilihan metode yang tepat bergantung pada jenis data dan asumsi yang dipenuhi.
Perbandingan Metode Analisis Korelasi
Tabel berikut membandingkan tiga metode analisis korelasi yang umum digunakan, meliputi kekuatan dan kelemahan masing-masing.
| Metode | Kekuatan | Kelemahan | Jenis Data |
|---|---|---|---|
| Korelasi Pearson | Mudah diinterpretasi, memberikan ukuran kekuatan dan arah hubungan yang tepat, banyak digunakan dan dipahami luas. | Membutuhkan data yang berdistribusi normal, sensitif terhadap outlier. | Data interval atau rasio |
| Korelasi Spearman | Tidak memerlukan data yang berdistribusi normal, lebih robust terhadap outlier. | Kurang efisien dibandingkan korelasi Pearson jika data berdistribusi normal, ukuran kekuatan hubungan kurang presisi. | Data ordinal atau data interval/rasio yang tidak berdistribusi normal |
| Korelasi Kendall | Robust terhadap outlier, lebih mudah diinterpretasikan daripada korelasi Spearman untuk sampel yang kecil. | Kurang efisien dibandingkan korelasi Pearson jika data berdistribusi normal, perhitungannya lebih kompleks. | Data ordinal atau data interval/rasio yang tidak berdistribusi normal |
Ilustrasi Analisis Korelasi: Penjualan Produk dan Jumlah Iklan
Mari kita bayangkan sebuah perusahaan yang ingin menganalisis hubungan antara jumlah iklan yang ditayangkan dan jumlah penjualan produknya. Data yang dikumpulkan mencakup jumlah iklan yang ditayangkan (dalam ribuan) dan jumlah unit produk yang terjual selama 10 bulan terakhir.
Misalnya, data yang diperoleh adalah sebagai berikut:
| Bulan | Jumlah Iklan (ribuan) | Jumlah Penjualan (unit) |
|---|---|---|
| Januari | 10 | 1000 |
| Februari | 12 | 1200 |
| Maret | 15 | 1500 |
| April | 18 | 1700 |
| Mei | 20 | 1900 |
| Juni | 17 | 1600 |
| Juli | 22 | 2100 |
| Agustus | 25 | 2400 |
| September | 23 | 2200 |
| Oktober | 28 | 2600 |
Dengan menggunakan analisis korelasi Pearson (karena data diasumsikan berdistribusi normal dan merupakan data interval), kita dapat menghitung koefisien korelasi. Anggaplah hasil analisis menunjukkan koefisien korelasi sebesar 0.95. Nilai ini menandakan adanya korelasi positif yang sangat kuat antara jumlah iklan yang ditayangkan dan jumlah penjualan produk. Artinya, semakin banyak iklan yang ditayangkan, semakin banyak pula produk yang terjual.
Namun, penting diingat bahwa korelasi ini tidak membuktikan hubungan sebab-akibat. Faktor lain mungkin juga berkontribusi terhadap peningkatan penjualan.
Interpretasi Koefisien Korelasi
Koefisien korelasi (r) merupakan ukuran statistik yang menunjukkan kekuatan dan arah hubungan linier antara dua variabel. Nilai koefisien korelasi berkisar antara -1 hingga +1. Pemahaman yang tepat tentang interpretasi nilai r sangat krusial dalam menarik kesimpulan yang valid dari analisis korelasi.
Arti dan Interpretasi Nilai Koefisien Korelasi (r)
Nilai r menunjukan kekuatan dan arah hubungan linier antara dua variabel. Semakin mendekati +1 atau -1, semakin kuat hubungannya. Nilai mendekati 0 mengindikasikan hubungan yang lemah atau tidak ada hubungan linier.
Perbedaan Korelasi Positif, Negatif, dan Tidak Ada Korelasi
Korelasi positif (r > 0) menunjukkan bahwa ketika satu variabel meningkat, variabel lainnya cenderung meningkat pula. Korelasi negatif (r < 0) menunjukkan bahwa ketika satu variabel meningkat, variabel lainnya cenderung menurun. Ketiadaan korelasi (r ≈ 0) menunjukkan tidak ada hubungan linier yang signifikan antara kedua variabel.
Contoh Interpretasi Nilai Koefisien Korelasi, Analisis korelasi
- r = 0.8: Menunjukkan korelasi positif yang kuat. Artinya, terdapat hubungan yang kuat di mana peningkatan pada satu variabel diiringi peningkatan pada variabel lainnya.
- r = -0.5: Menunjukkan korelasi negatif yang sedang. Artinya, terdapat hubungan sedang di mana peningkatan pada satu variabel diiringi penurunan pada variabel lainnya.
- r = 0.1: Menunjukkan korelasi positif yang sangat lemah. Artinya, hampir tidak ada hubungan linier yang signifikan antara kedua variabel.
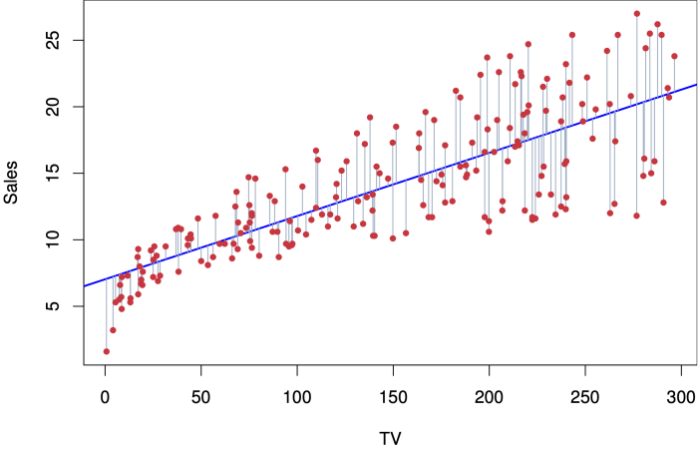
Visualisasi Grafik Scatter Plot
Grafik scatter plot memberikan representasi visual yang efektif dari hubungan antara dua variabel. Berikut deskripsi visual berbagai tingkat korelasi:
- Korelasi Positif Kuat (misalnya, r = 0.8): Titik-titik data akan terkonsentrasi di sekitar garis lurus yang miring ke atas dari kiri bawah ke kanan atas. Sebagian besar titik akan berada dekat dengan garis tersebut.
- Korelasi Negatif Sedang (misalnya, r = -0.5): Titik-titik data akan terkonsentrasi di sekitar garis lurus yang miring ke bawah dari kiri atas ke kanan bawah. Titik-titik akan lebih tersebar dibandingkan dengan korelasi kuat.
- Korelasi Lemah atau Tidak Ada (misalnya, r = 0.1 atau r ≈ 0): Titik-titik data akan tersebar secara acak tanpa pola yang jelas. Tidak akan terlihat garis lurus yang jelas yang mewakili tren data.
Pentingnya Mempertimbangkan Faktor Lain
Meskipun koefisien korelasi memberikan informasi berharga tentang hubungan antara dua variabel, penting untuk diingat bahwa korelasi bukan berarti kausalitas. Hubungan antara dua variabel dapat dipengaruhi oleh faktor-faktor lain yang tidak diukur dalam analisis. Interpretasi koefisien korelasi harus dilakukan dengan hati-hati dan mempertimbangkan konteks penelitian secara menyeluruh.
Pengujian Signifikansi Korelasi

Setelah menghitung koefisien korelasi, langkah selanjutnya adalah menguji seberapa signifikan korelasi tersebut. Artinya, kita perlu memastikan apakah korelasi yang ditemukan bukan hanya kebetulan semata, melainkan mencerminkan hubungan nyata antara dua variabel yang diteliti. Pengujian ini penting untuk menghindari kesimpulan yang salah berdasarkan data yang mungkin hanya acak.
Pengujian signifikansi korelasi menggunakan pendekatan pengujian hipotesis. Kita akan membandingkan koefisien korelasi yang kita hitung dengan nilai yang diharapkan jika tidak ada korelasi (hipotesis nol). Jika perbedaannya cukup besar, kita akan menolak hipotesis nol dan menyimpulkan bahwa korelasi tersebut signifikan secara statistik.
Uji Statistik untuk Signifikansi Korelasi
Uji statistik yang umum digunakan untuk menguji signifikansi korelasi adalah uji t. Uji t ini menguji apakah koefisien korelasi yang diperoleh secara signifikan berbeda dari nol. Nilai t dihitung berdasarkan koefisien korelasi (r), ukuran sampel (n), dan derajat kebebasan (df = n-2). Semakin besar nilai t, semakin kuat bukti bahwa korelasi tersebut signifikan.
Interpretasi Nilai p-value
Nilai p-value merupakan probabilitas mendapatkan hasil sekurang-kurangnya sebaik hasil yang diperoleh, dengan asumsi hipotesis nol benar (tidak ada korelasi). Nilai p-value ini dibandingkan dengan tingkat signifikansi (α), yang biasanya ditetapkan pada 0.05. Jika nilai p-value kurang dari α (misalnya, p < 0.05), maka hipotesis nol ditolak, dan korelasi dinyatakan signifikan secara statistik. Sebaliknya, jika p-value lebih besar dari α, maka hipotesis nol gagal ditolak, dan korelasi dianggap tidak signifikan.
Contoh Perhitungan Pengujian Signifikansi Korelasi
Misalkan kita memiliki data tentang tinggi badan (x) dan berat badan (y) dari 10 orang. Setelah menghitung, kita memperoleh koefisien korelasi r = 0.8. Dengan derajat kebebasan (df) = 10-2 = 8, dan menggunakan tabel distribusi t atau software statistik, kita dapat mencari nilai t kritis dan nilai p-value. Misalnya, nilai t hitung sebesar 3,36 dan nilai p-value sebesar 0,01.
Karena p-value (0,01) < α (0,05), maka kita menolak hipotesis nol dan menyimpulkan bahwa terdapat korelasi yang signifikan antara tinggi dan berat badan.
Langkah-langkah Pengujian Signifikansi Korelasi
| Langkah | Deskripsi | Rumus/Perhitungan | Interpretasi |
|---|---|---|---|
| 1. Hitung koefisien korelasi (r) | Hitung koefisien korelasi Pearson antara dua variabel. | Rumus perhitungan koefisien korelasi Pearson | Menunjukkan kekuatan dan arah hubungan antara dua variabel. |
| 2. Tentukan tingkat signifikansi (α) | Biasanya ditetapkan pada 0.05. | α = 0.05 | Tingkat kepercayaan untuk menolak hipotesis nol. |
| 3. Hitung nilai t | Gunakan rumus uji t untuk korelasi. | t = r√[(n-2)/(1-r²)] | Nilai t yang diperoleh dibandingkan dengan nilai t kritis. |
| 4. Tentukan nilai p-value | Cari nilai p-value menggunakan tabel distribusi t atau software statistik, berdasarkan nilai t dan derajat kebebasan (df = n-2). | Menggunakan tabel distribusi t atau software statistik | Probabilitas mendapatkan hasil sekurang-kurangnya sebaik hasil yang diperoleh, dengan asumsi hipotesis nol benar. |
| 5. Bandingkan p-value dengan α | Jika p-value < α, tolak hipotesis nol; jika p-value ≥ α, gagal tolak hipotesis nol. | p-value vs α | Kesimpulan tentang signifikansi korelasi. |
Pembatasan Analisis Korelasi

Analisis korelasi merupakan alat statistik yang ampuh untuk mengidentifikasi hubungan antara dua variabel atau lebih. Namun, penting untuk memahami bahwa analisis korelasi memiliki keterbatasan dan tidak boleh diinterpretasikan secara berlebihan. Memahami batasan ini krusial untuk menghindari kesimpulan yang salah dan menyesatkan.
Hubungan Korelasi Bukan Implikasi Sebab-Akibat
Salah satu keterbatasan utama analisis korelasi adalah ketidakmampuannya untuk membuktikan hubungan sebab-akibat. Meskipun terdapat korelasi yang kuat antara dua variabel, hal ini tidak secara otomatis berarti satu variabel menyebabkan perubahan pada variabel lainnya. Korelasi hanya menunjukkan adanya hubungan, bukan sebab dan akibat. Contohnya, korelasi positif antara penjualan es krim dan kasus tenggelam tidak berarti es krim menyebabkan orang tenggelam.
Keduanya dipengaruhi oleh variabel ketiga, yaitu cuaca panas.
Potensi Bias dan Kesalahan Interpretasi
Beberapa faktor dapat menyebabkan bias dan kesalahan interpretasi dalam analisis korelasi. Ukuran sampel yang kecil, misalnya, dapat menghasilkan hasil yang tidak akurat dan menyesatkan. Selain itu, penggunaan data yang tidak representatif atau adanya outlier (data yang menyimpang jauh dari data lainnya) juga dapat mempengaruhi hasil analisis. Perlu kehati-hatian dalam memilih dan membersihkan data sebelum melakukan analisis korelasi.
Variabel Pengganggu (Confounding Variables)
Variabel pengganggu adalah variabel lain yang tidak dipertimbangkan dalam analisis, namun dapat mempengaruhi hubungan antara variabel yang diteliti. Kehadiran variabel pengganggu dapat menyebabkan korelasi yang diamati menjadi bias atau bahkan menyesatkan. Mengidentifikasi dan mengendalikan variabel pengganggu merupakan langkah penting dalam analisis korelasi untuk mendapatkan hasil yang lebih akurat dan valid.
Contoh Kasus Menyesatkan
Misalnya, penelitian menunjukkan korelasi positif antara jumlah dokter dan angka kematian di suatu wilayah. Interpretasi yang naif mungkin menyimpulkan bahwa banyaknya dokter menyebabkan peningkatan angka kematian. Namun, variabel pengganggu yang lebih masuk akal adalah tingkat kesehatan penduduk di wilayah tersebut. Wilayah dengan tingkat kesehatan yang buruk cenderung memiliki lebih banyak dokter dan angka kematian yang lebih tinggi.
Pentingnya Analisis Statistik Lain
“Analisis korelasi hanyalah satu bagian dari teka-teki. Untuk memahami hubungan yang kompleks, perlu dipadukan dengan metode analisis statistik lain seperti regresi, analisis jalur, atau eksperimen terkontrol untuk menguji hubungan sebab-akibat.”
Kutipan di atas menyoroti pentingnya tidak mengandalkan hanya pada analisis korelasi. Metode-metode lain dapat membantu mengklarifikasi hubungan antara variabel dan mengendalikan pengaruh variabel pengganggu, sehingga memberikan gambaran yang lebih lengkap dan akurat.
Aplikasi Analisis Korelasi dalam Studi Kasus
Analisis korelasi merupakan alat statistik yang ampuh untuk mengungkap hubungan antara dua variabel atau lebih. Pemahaman tentang korelasi sangat penting dalam berbagai bidang, mulai dari ekonomi dan keuangan hingga kesehatan dan lingkungan. Studi kasus berikut akan mendemonstrasikan penerapan analisis korelasi dalam konteks yang mudah dipahami, menunjukkan langkah-langkah analisis dan interpretasi hasilnya.
Studi Kasus: Hubungan Antara Jam Belajar dan Nilai Ujian
Studi kasus ini meneliti hubungan antara jumlah jam belajar per minggu (variabel X) dan nilai ujian akhir mata pelajaran Matematika (variabel Y) pada sekelompok siswa. Data dikumpulkan dari 10 siswa, dengan nilai ujian berkisar antara 0 hingga 100.
Persiapan Data dan Pemilihan Metode
Data yang dikumpulkan disajikan dalam tabel berikut. Metode analisis korelasi yang digunakan adalah Korelasi Pearson, karena data berdistribusi normal dan memiliki skala interval.
| Siswa | Jam Belajar (X) | Nilai Ujian (Y) |
|---|---|---|
| 1 | 5 | 60 |
| 2 | 10 | 75 |
| 3 | 15 | 85 |
| 4 | 20 | 90 |
| 5 | 8 | 70 |
| 6 | 12 | 80 |
| 7 | 18 | 88 |
| 8 | 6 | 65 |
| 9 | 14 | 82 |
| 10 | 22 | 95 |
Hasil Analisis dan Interpretasi
Setelah melakukan perhitungan korelasi Pearson, diperoleh nilai koefisien korelasi (r) sebesar 0.92. Nilai ini menunjukkan korelasi positif yang kuat antara jam belajar dan nilai ujian. Semakin banyak jam belajar, semakin tinggi nilai ujian yang cenderung diperoleh. Hal ini sesuai dengan intuisi bahwa dedikasi belajar berpengaruh positif terhadap prestasi akademik.
Kesimpulan Analisis Korelasi
- Terdapat korelasi positif yang kuat antara jam belajar dan nilai ujian Matematika.
- Peningkatan jam belajar dikaitkan dengan peningkatan nilai ujian.
- Hasil ini mendukung hipotesis bahwa dedikasi belajar memiliki pengaruh signifikan terhadap prestasi akademik.
Representasi Grafik
Grafik scatter plot akan menampilkan titik-titik data yang merepresentasikan pasangan nilai jam belajar dan nilai ujian masing-masing siswa. Garis tren (garis regresi) yang ditarik melalui titik-titik data akan menunjukkan arah dan kekuatan hubungan korelasi. Kemiringan garis yang positif dan mendekati nilai 1 menunjukkan korelasi positif yang kuat, sesuai dengan nilai r = 0.92 yang telah dihitung. Semakin rapat titik-titik data berada di sekitar garis tren, semakin kuat korelasinya.
Grafik ini secara visual mengkonfirmasi adanya hubungan positif dan kuat antara variabel jam belajar dan nilai ujian.
Kesimpulan
Analisis korelasi, meskipun bermanfaat, memiliki keterbatasan. Ia menunjukkan hubungan, bukan sebab-akibat. Interpretasi yang cermat, mempertimbangkan variabel pengganggu dan konteks data, sangat penting untuk menghindari kesimpulan yang keliru. Dengan memahami kekuatan dan kelemahannya, dan menggabungkannya dengan metode analisis lain, analisis korelasi menjadi alat yang berharga dalam pengambilan keputusan berbasis data di berbagai bidang, mulai dari bisnis hingga ilmu sosial.