Analisis Regresi Linier Sederhana merupakan metode statistik yang powerful untuk mengungkap hubungan antara dua variabel. Bayangkan Anda ingin memprediksi harga rumah berdasarkan luasnya; regresi linier sederhana dapat membantu! Metode ini mencari garis lurus terbaik yang merepresentasikan hubungan antara variabel dependen (harga rumah) dan variabel independen (luas rumah). Dengan memahami prinsip-prinsip dasar regresi linier sederhana, Anda dapat menganalisis data, membuat prediksi, dan mengambil keputusan yang lebih baik berdasarkan data yang ada.
Topik ini akan membahas pengertian regresi linier sederhana, asumsinya, perhitungan dan interpretasi koefisien, pengujian hipotesis, serta penerapannya menggunakan software statistik. Kita akan menjelajahi langkah demi langkah, dari memahami definisi hingga menginterpretasi hasil analisis, sehingga Anda dapat mengaplikasikannya dalam berbagai konteks.
Regresi Linier Sederhana
Regresi linier sederhana merupakan teknik statistik yang digunakan untuk memodelkan hubungan linier antara dua variabel. Metode ini membantu kita memahami bagaimana perubahan pada satu variabel (variabel independen) mempengaruhi variabel lainnya (variabel dependen). Dengan kata lain, regresi linier sederhana membantu kita memprediksi nilai variabel dependen berdasarkan nilai variabel independen.
Contoh Penerapan Regresi Linier Sederhana
Bayangkan seorang pemilik toko ingin memprediksi jumlah penjualan berdasarkan jumlah iklan yang dipasang. Jumlah iklan yang dipasang adalah variabel independen (X), sementara jumlah penjualan adalah variabel dependen (Y). Dengan menggunakan regresi linier sederhana, pemilik toko dapat membangun model yang menghubungkan kedua variabel tersebut, sehingga dapat memperkirakan penjualan berdasarkan jumlah iklan yang direncanakan.
Identifikasi Variabel Dependen dan Independen
Dalam regresi linier sederhana, sangat penting untuk mengidentifikasi dengan tepat variabel dependen dan independen. Variabel dependen (Y) adalah variabel yang ingin kita prediksi atau jelaskan. Variabel independen (X) adalah variabel yang digunakan untuk memprediksi variabel dependen. Dalam contoh penjualan toko di atas, jumlah penjualan (Y) bergantung pada jumlah iklan (X).
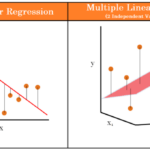
Perbandingan Regresi Linier Sederhana dengan Metode Statistik Lainnya
Regresi linier sederhana merupakan salah satu dari sekian banyak metode statistik yang dapat digunakan untuk menganalisis data. Berikut perbandingannya dengan beberapa metode lain:
| Metode | Deskripsi Singkat | Keunggulan | Kekurangan |
|---|---|---|---|
| Regresi Linier Sederhana | Memmodelkan hubungan linier antara dua variabel. | Mudah dipahami dan diinterpretasi; implementasinya relatif mudah. | Hanya dapat menangani hubungan linier; asumsi-asumsi tertentu harus dipenuhi (misalnya, normalitas residual). |
| Regresi Linier Berganda | Memmodelkan hubungan linier antara satu variabel dependen dan dua atau lebih variabel independen. | Dapat menangani hubungan yang lebih kompleks dibandingkan regresi linier sederhana. | Lebih kompleks untuk diinterpretasi dan implementasinya lebih rumit. |
| Korelasi | Mengukur kekuatan dan arah hubungan antara dua variabel. | Memberikan gambaran singkat tentang hubungan antara dua variabel. | Tidak dapat digunakan untuk prediksi; hanya menunjukkan hubungan, bukan sebab-akibat. |
| Analisis Varian (ANOVA) | Membandingkan rata-rata dari dua atau lebih kelompok. | Cocok untuk membandingkan perbedaan rata-rata antar kelompok. | Tidak dapat digunakan untuk memprediksi nilai variabel dependen. |
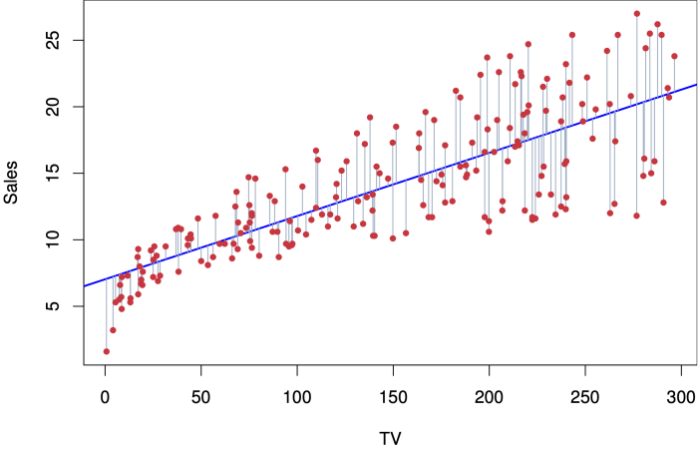
Ilustrasi Hubungan Variabel dan Garis Regresi
Hubungan antara variabel dependen (Y) dan independen (X) dalam regresi linier sederhana dapat divisualisasikan sebagai titik-titik pada diagram pencar. Garis regresi, yang merupakan garis lurus terbaik yang mendekati titik-titik tersebut, merepresentasikan hubungan linier antara kedua variabel. Kemiringan garis regresi menunjukkan kekuatan dan arah hubungan; semakin curam kemiringan, semakin kuat hubungannya. Jika kemiringan positif, maka peningkatan X diiringi peningkatan Y, dan sebaliknya.
Garis regresi memberikan estimasi nilai Y untuk setiap nilai X yang diberikan.
Sebagai contoh, jika kita menggambarkan titik-titik data penjualan toko (Y) terhadap jumlah iklan (X), garis regresi akan menunjukkan tren umum hubungan antara keduanya. Jika garis regresi memiliki kemiringan positif, maka dapat disimpulkan bahwa peningkatan jumlah iklan cenderung meningkatkan jumlah penjualan.
Asumsi Regresi Linier Sederhana
Regresi linier sederhana, meskipun tampak sederhana, bergantung pada beberapa asumsi kunci agar hasil analisisnya valid dan dapat diinterpretasi dengan benar. Pelanggaran terhadap asumsi-asumsi ini dapat menyebabkan bias dalam estimasi parameter, kesalahan standar yang tidak akurat, dan kesimpulan yang salah. Oleh karena itu, pemahaman dan pengecekan terhadap asumsi-asumsi ini merupakan langkah krusial dalam analisis regresi linier sederhana.
Lima Asumsi Dasar Regresi Linier Sederhana
Lima asumsi utama yang mendasari regresi linier sederhana adalah linearitas, independensi, normalitas, homoskedastisitas, dan tidak adanya outliers yang signifikan. Kelima asumsi ini saling berkaitan dan perlu dipenuhi untuk memastikan keakuratan dan reliabilitas model.
- Linearitas: Hubungan antara variabel dependen (Y) dan variabel independen (X) bersifat linear. Artinya, perubahan pada X akan menyebabkan perubahan proporsional pada Y. Pelanggaran asumsi ini dapat menghasilkan model yang tidak akurat dan tidak mampu menangkap pola hubungan yang sebenarnya, misalnya hubungan yang berbentuk kurva.
- Independensi: Observasi dalam data bersifat independen satu sama lain. Artinya, nilai Y pada satu observasi tidak memengaruhi nilai Y pada observasi lain. Pelanggaran asumsi ini sering terjadi pada data time series, di mana observasi berurutan cenderung berkorelasi. Ini dapat menyebabkan pengurangan efisiensi estimasi parameter.
- Normalitas: Residuals (selisih antara nilai aktual Y dan nilai Y yang diprediksi oleh model) terdistribusi normal. Asumsi ini penting untuk pengujian signifikansi parameter dan interval kepercayaan. Pelanggaran asumsi ini dapat menyebabkan kesalahan dalam pengujian hipotesis dan interval kepercayaan yang tidak akurat. Misalnya, jika residual tidak normal, pengujian t untuk koefisien regresi mungkin tidak valid.
- Homoskedastisitas: Variansi dari residuals konstan untuk semua nilai X. Artinya, penyebaran residuals di sekitar garis regresi sama untuk semua nilai X. Heteroskedastisitas (pelanggaran asumsi ini) dapat menyebabkan estimasi parameter yang tidak efisien dan kesalahan standar yang bias.
- Tidak Adanya Outliers yang Signifikan: Tidak ada observasi yang memiliki pengaruh yang tidak proporsional terhadap garis regresi. Outliers dapat menyebabkan bias dalam estimasi parameter dan mempengaruhi interpretasi model secara keseluruhan. Pengaruh outliers dapat dideteksi melalui analisis diagnostik seperti leverage dan Cook’s distance.
Pemeriksaan Pemenuhan Asumsi
Pemeriksaan terhadap pemenuhan asumsi regresi linier sederhana dapat dilakukan melalui beberapa metode. Metode visual seperti scatter plot dan histogram, serta uji statistik formal, dapat digunakan untuk mengevaluasi masing-masing asumsi.
- Linearitas: Dapat diperiksa melalui scatter plot antara variabel dependen dan independen. Jika hubungannya terlihat linear, asumsi terpenuhi. Jika terlihat pola non-linear, transformasi data mungkin diperlukan.
- Independensi: Dapat diperiksa melalui uji Durbin-Watson untuk data time series. Nilai Durbin-Watson mendekati 2 menunjukkan tidak ada autokorelasi.
- Normalitas: Dapat diperiksa melalui histogram atau Q-Q plot dari residuals. Uji formal seperti uji Shapiro-Wilk dapat digunakan untuk menguji normalitas residuals.
- Homoskedastisitas: Dapat diperiksa melalui scatter plot antara residuals dan nilai prediksi. Jika penyebaran residuals konstan, asumsi terpenuhi. Uji formal seperti uji Breusch-Pagan dapat digunakan.
- Tidak Adanya Outliers: Dapat diperiksa melalui scatter plot dan analisis diagnostik seperti leverage dan Cook’s distance. Observasi dengan leverage dan Cook’s distance yang tinggi perlu diperiksa lebih lanjut.
Penanganan Pelanggaran Asumsi
Jika asumsi regresi linier sederhana tidak terpenuhi, beberapa langkah dapat diambil untuk memperbaiki masalah tersebut. Langkah-langkah ini dapat berupa transformasi data, penggunaan model regresi alternatif, atau penghapusan observasi yang melanggar asumsi.
- Transformasi Data: Transformasi logaritma atau pangkat dapat digunakan untuk menstabilkan variansi dan mendekati linearitas.
- Model Regresi Alternatif: Jika linearitas tidak terpenuhi, model regresi non-linear mungkin lebih sesuai.
- Penghapusan Observasi: Outliers yang signifikan dapat dihapus jika ada alasan yang kuat untuk mempercayai bahwa mereka merupakan kesalahan pengukuran atau observasi yang tidak representatif.
- Penggunaan teknik robust regression: Teknik ini kurang sensitif terhadap pelanggaran asumsi normalitas dan homoskedastisitas.
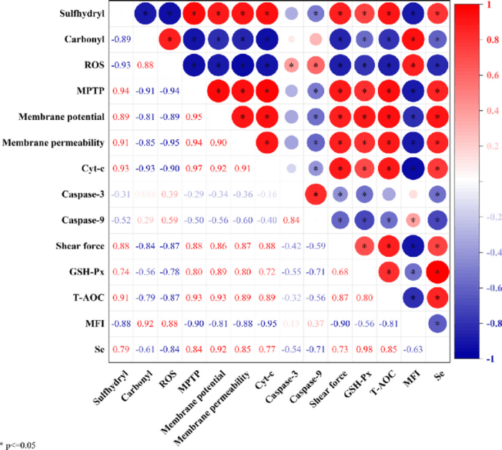
Implikasi Pelanggaran Multikolinearitas
Multikolinearitas, meskipun bukan salah satu dari lima asumsi utama yang telah dibahas, merupakan masalah yang sering terjadi dalam regresi linier berganda (bukan sederhana). Keberadaan korelasi yang tinggi antar variabel independen dapat menyebabkan estimasi parameter yang tidak stabil, kesalahan standar yang besar, dan kesulitan dalam menginterpretasi koefisien regresi. Dalam kasus ekstrem, multikolinearitas dapat membuat model tidak dapat diestimasi sama sekali.
Perhitungan dan Interpretasi Koefisien Regresi

Analisis regresi linier sederhana bertujuan untuk memodelkan hubungan linier antara dua variabel, yaitu variabel dependen (Y) dan variabel independen (X). Koefisien regresi, yang terdiri dari konstanta (a) dan koefisien regresi (b), merupakan kunci untuk memahami model ini. Koefisien-koefisien ini memberikan informasi penting tentang bagaimana perubahan pada variabel independen mempengaruhi variabel dependen. Selain itu, koefisien determinasi (R-squared) membantu kita menilai seberapa baik model tersebut menjelaskan variasi data.
Rumus dan Perhitungan Koefisien Regresi
Koefisien regresi dihitung menggunakan rumus berikut. Rumus ini didapatkan melalui metode kuadrat terkecil ( least squares method) yang meminimalkan jumlah kuadrat dari selisih antara nilai observasi dan nilai prediksi.
b = Σ[(Xi – X̄)(Yi – Ȳ)] / Σ[(Xi – X̄)²]
a = Ȳ – bX̄
dimana:
- b adalah koefisien regresi (kemiringan garis regresi)
- a adalah konstanta (intercept)
- Xi adalah nilai observasi variabel independen
- Yi adalah nilai observasi variabel dependen
- X̄ adalah rata-rata variabel independen
- Ȳ adalah rata-rata variabel dependen
Sebagai contoh, misalkan kita memiliki data berikut tentang jumlah jam belajar (X) dan nilai ujian (Y) dari 5 siswa:
| Jam Belajar (X) | Nilai Ujian (Y) |
|---|---|
| 2 | 60 |
| 4 | 70 |
| 6 | 80 |
| 8 | 90 |
| 10 | 100 |
Dengan menggunakan rumus di atas dan melakukan perhitungan, kita akan mendapatkan nilai a dan b. Proses perhitungan ini melibatkan beberapa langkah, termasuk menghitung rata-rata X dan Y, serta menghitung jumlah kuadrat dan perkalian silang. Hasil perhitungan akan menghasilkan nilai a (konstanta) dan b (kemiringan). Misalnya, setelah perhitungan, kita peroleh a = 50 dan b = 5. Ini berarti persamaan regresi liniernya adalah Y = 50 + 5X.
Interpretasi Koefisien Regresi
Dalam contoh di atas, nilai b = 5 mengindikasikan bahwa setiap penambahan satu jam belajar diprediksi akan meningkatkan nilai ujian sebesar 5 poin. Nilai a = 50 merepresentasikan nilai ujian yang diprediksi jika jam belajar sama dengan nol. Interpretasi ini tentunya bergantung pada konteks permasalahan yang sedang dikaji. Penting untuk diingat bahwa interpretasi ini hanya berlaku dalam rentang data yang digunakan untuk membangun model.
Perhitungan dan Interpretasi Koefisien Determinasi (R-squared)
Koefisien determinasi (R-squared) mengukur proporsi variasi dalam variabel dependen (Y) yang dapat dijelaskan oleh variabel independen (X) dalam model regresi. Nilai R-squared berkisar antara 0 dan 1. Semakin tinggi nilai R-squared, semakin baik model regresi dalam menjelaskan variasi data.
R-squared dihitung dengan rumus:
R² = SSR / SST
dimana:
- SSR (Sum of Squares Regression) adalah jumlah kuadrat regresi, yang mengukur variasi dalam Y yang dijelaskan oleh model.
- SST (Sum of Squares Total) adalah jumlah kuadrat total, yang mengukur total variasi dalam Y.
Misalnya, jika R-squared adalah 0.8, maka 80% variasi dalam nilai ujian dapat dijelaskan oleh jumlah jam belajar. Sisa 20% variasi disebabkan oleh faktor-faktor lain yang tidak termasuk dalam model.
Prediksi Nilai Variabel Dependen
Setelah model regresi dibangun, kita dapat menggunakannya untuk memprediksi nilai variabel dependen (Y) berdasarkan nilai variabel independen (X). Dalam contoh kita, jika seorang siswa belajar selama 7 jam, kita dapat memprediksi nilai ujiannya dengan mensubstitusikan X = 7 ke dalam persamaan regresi: Y = 50 + 5(7) = 85. Prediksi ini hanya merupakan estimasi, dan nilai aktual mungkin berbeda.
Pengujian Hipotesis
Setelah model regresi linier sederhana dibangun, langkah selanjutnya adalah menguji signifikansi model dan koefisien regresi. Pengujian hipotesis ini bertujuan untuk menentukan apakah hubungan antara variabel dependen dan independen signifikan secara statistik, atau hanya terjadi secara kebetulan.
Pengujian ini dilakukan dengan menguji hipotesis nol (H0) yang menyatakan tidak ada hubungan antara variabel, melawan hipotesis alternatif (H1) yang menyatakan ada hubungan antara variabel. Untuk koefisien regresi, kita akan menggunakan uji t.
Uji t untuk Koefisien Regresi
Uji t digunakan untuk menguji signifikansi koefisien regresi (b). Nilai t dihitung dengan membagi koefisien regresi dengan standar errornya. Rumusnya adalah:
t = b / SE(b)
di mana:
- b adalah koefisien regresi
- SE(b) adalah standar error dari koefisien regresi
Setelah nilai t dihitung, kita membandingkannya dengan nilai kritis t pada tingkat signifikansi tertentu (misalnya, α = 0.05) dan derajat kebebasan (df = n – 2, di mana n adalah jumlah observasi). Kita juga dapat melihat p-value yang dihasilkan dari perhitungan uji t. P-value menunjukkan probabilitas mendapatkan hasil sekurang-kurangnya sebaik hasil yang diamati, dengan asumsi hipotesis nol benar.
Contoh Perhitungan Nilai t dan p-value
Misalnya, setelah melakukan analisis regresi, kita mendapatkan koefisien regresi (b) sebesar 2.5 dan standar errornya (SE(b)) sebesar 0.
8. Maka nilai t adalah:
t = 2.5 / 0.8 = 3.125
Dengan asumsi derajat kebebasan 28 (n=30) dan tingkat signifikansi 0.05, nilai kritis t adalah sekitar 2.048. Karena nilai t hitung (3.125) lebih besar dari nilai kritis t (2.048), kita menolak hipotesis nol. Atau, jika p-value yang dihasilkan kurang dari 0.05, kita juga menolak hipotesis nol. Ini mengindikasikan bahwa koefisien regresi signifikan secara statistik.
Interpretasi Hasil Pengujian Hipotesis, Analisis regresi linier sederhana
Jika hipotesis nol ditolak (p-value < α), berarti terdapat bukti yang cukup untuk menyimpulkan bahwa terdapat hubungan yang signifikan secara statistik antara variabel independen dan dependen. Sebaliknya, jika hipotesis nol gagal ditolak (p-value ≥ α), berarti tidak ada bukti yang cukup untuk menyimpulkan adanya hubungan yang signifikan secara statistik.
Penting untuk diingat bahwa signifikansi statistik tidak selalu berarti signifikansi praktis. Suatu hubungan mungkin signifikan secara statistik tetapi efeknya mungkin terlalu kecil untuk memiliki implikasi praktis yang berarti.
Menentukan Signifikansi Statistik Model Regresi
Selain menguji signifikansi koefisien regresi, kita juga perlu menguji signifikansi model regresi secara keseluruhan. Ini dapat dilakukan dengan menggunakan uji F. Uji F membandingkan varians yang dijelaskan oleh model dengan varians yang tidak dijelaskan oleh model. Nilai F yang tinggi menunjukkan bahwa model menjelaskan sebagian besar varians dalam data, dan model signifikan secara statistik.
- Hitung nilai F statistik menggunakan software statistik.
- Tentukan derajat kebebasan untuk numerator (jumlah prediktor) dan denominator (jumlah observasi dikurangi jumlah prediktor dikurangi 1).
- Bandingkan nilai F statistik dengan nilai kritis F pada tingkat signifikansi yang dipilih (misalnya, α = 0.05).
- Jika nilai F statistik lebih besar dari nilai kritis F, tolak hipotesis nol dan simpulkan bahwa model regresi signifikan secara statistik.
Signifikansi Statistik vs. Signifikansi Praktis
Signifikansi statistik menunjukkan bahwa hasil yang ditemukan tidak mungkin terjadi secara kebetulan. Namun, signifikansi praktis mengacu pada pentingnya hasil tersebut dalam konteks nyata. Suatu hubungan mungkin signifikan secara statistik tetapi efeknya mungkin terlalu kecil untuk dipertimbangkan dalam pengambilan keputusan. Misalnya, koefisien regresi mungkin signifikan secara statistik, tetapi perubahan kecil pada variabel independen hanya menyebabkan perubahan yang sangat kecil pada variabel dependen, sehingga kurang relevan dalam praktik.
Penerapan Regresi Linier Sederhana Menggunakan Software Statistik
Analisis regresi linier sederhana, meskipun dapat dihitung manual, akan jauh lebih efisien dan akurat jika dilakukan dengan bantuan software statistik. Software ini mampu menangani data dalam jumlah besar, melakukan perhitungan kompleks dengan cepat, dan menghasilkan visualisasi data yang membantu interpretasi. Pilihan software yang tepat akan mempermudah proses analisis dan meningkatkan kualitas hasil.
Software Statistik untuk Analisis Regresi Linier Sederhana
Beberapa software statistik populer yang dapat digunakan untuk analisis regresi linier sederhana antara lain SPSS, R, Python (dengan library seperti statsmodels atau scikit-learn), dan Excel (dengan fitur Data Analysis). Setiap software memiliki kelebihan dan kekurangan masing-masing, tergantung pada kebutuhan dan keahlian pengguna.
Langkah-langkah Analisis Regresi Linier Sederhana Menggunakan SPSS
Berikut langkah-langkah umum melakukan analisis regresi linier sederhana menggunakan SPSS. Perlu diingat bahwa langkah-langkah detail mungkin sedikit berbeda tergantung versi SPSS yang digunakan.
- Masukkan data ke dalam SPSS. Pastikan variabel dependen dan independen telah didefinisikan dengan benar.
- Buka menu Analyze > Regression > Linear.
- Pindahkan variabel dependen ke kotak Dependent dan variabel independen ke kotak Independent(s).
- Klik tombol Options dan pilih statistik yang diinginkan, seperti koefisien regresi, R-squared, dan uji signifikansi.
- Klik OK untuk menjalankan analisis.
Interpretasi Output SPSS
Setelah analisis selesai, SPSS akan menampilkan output yang berisi berbagai statistik. Beberapa statistik penting yang perlu diperhatikan adalah:
- Koefisien regresi (b): Menunjukkan besarnya pengaruh variabel independen terhadap variabel dependen. Nilai b positif menunjukkan hubungan positif, sedangkan nilai b negatif menunjukkan hubungan negatif.
- Konstanta (a): Menunjukkan nilai variabel dependen ketika variabel independen bernilai nol.
- R-squared: Menunjukkan proporsi variansi variabel dependen yang dapat dijelaskan oleh variabel independen. Nilai R-squared yang tinggi menunjukkan model regresi yang baik.
- Uji signifikansi (p-value): Menunjukkan probabilitas bahwa hasil analisis terjadi secara kebetulan. Nilai p-value yang kurang dari 0.05 umumnya dianggap signifikan secara statistik.
Contoh Output SPSS dan Interpretasinya
Misalkan kita menganalisis hubungan antara jumlah jam belajar (variabel independen) dan nilai ujian (variabel dependen). Output SPSS mungkin menunjukkan koefisien regresi b = 2, konstanta a = 50, R-squared = 0.8, dan p-value = 0.01. Ini berarti setiap penambahan satu jam belajar diprediksi akan meningkatkan nilai ujian sebesar 2 poin, nilai ujian ketika tidak belajar adalah 50, 80% variansi nilai ujian dapat dijelaskan oleh jumlah jam belajar, dan hubungan antara jam belajar dan nilai ujian signifikan secara statistik.
| Koefisien | B | Sig. |
|---|---|---|
| Konstanta | 50 | 0.000 |
| Jam Belajar | 2 | 0.010 |
| R-squared | 0.8 | |
Kelebihan dan Kekurangan Penggunaan Software Statistik
Software statistik memudahkan analisis regresi linier sederhana dengan menyediakan fitur perhitungan dan visualisasi yang canggih. Namun, pengguna perlu memahami prinsip-prinsip statistik dan interpretasi output untuk menghindari kesalahan interpretasi. Penggunaan software juga bergantung pada ketersediaan data yang akurat dan representatif.
Pemungkas: Analisis Regresi Linier Sederhana
Memahami dan mengaplikasikan analisis regresi linier sederhana membuka pintu bagi pemahaman yang lebih dalam tentang hubungan antar variabel. Meskipun memiliki keterbatasan, kemampuannya dalam memprediksi dan menganalisis data membuatnya menjadi alat yang sangat berharga dalam berbagai bidang. Dengan memahami asumsi-asumsinya dan cara menginterpretasi hasilnya, Anda dapat memanfaatkan kekuatan regresi linier sederhana untuk mengambil keputusan yang lebih data-driven dan efektif.