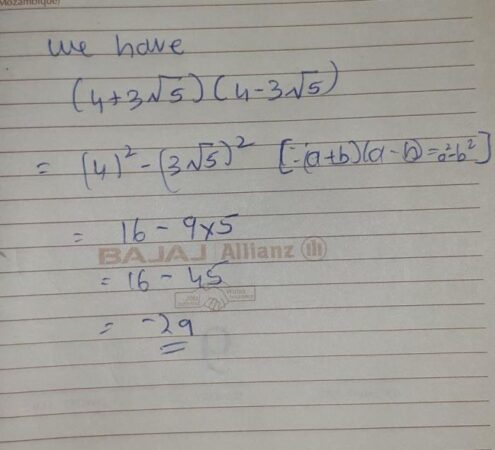Bentuk sederhana dari 15 per 4 akar 3 adalah pertanyaan yang sering muncul dalam matematika, khususnya dalam penyederhanaan ekspresi aljabar yang melibatkan akar. Memahami proses rasionalisasi penyebut sangat krusial untuk mencapai bentuk paling sederhana dan mempermudah perhitungan selanjutnya. Proses ini melibatkan manipulasi aljabar untuk menghilangkan akar dari penyebut pecahan, menghasilkan bentuk yang lebih ringkas dan mudah dipahami.
Artikel ini akan memandu Anda langkah demi langkah dalam menyederhanakan ekspresi “15 per 4 akar 3”, menjelaskan konsep rasionalisasi, dan menunjukkan penerapannya dalam konteks geometri. Kita akan mengeksplorasi nilai desimal dari bentuk sederhana tersebut dan membandingkannya dengan nilai desimal ekspresi awal. Selain itu, kita juga akan membahas kesalahan umum yang sering terjadi saat melakukan penyederhanaan ekspresi yang melibatkan akar.
Penyederhanaan Ekspresi Matematika
Penyederhanaan ekspresi matematika merupakan proses penting untuk menyajikan suatu ekspresi dalam bentuk yang lebih sederhana dan mudah dipahami. Proses ini sering melibatkan manipulasi aljabar dan teknik-teknik seperti rasionalisasi penyebut. Berikut akan diuraikan langkah-langkah penyederhanaan ekspresi “15 per 4 akar 3”, termasuk proses rasionalisasi penyebutnya.
Langkah-langkah Penyederhanaan Ekspresi 15/(4√3)
Ekspresi “15 per 4 akar 3” dapat ditulis sebagai 15/(4√3). Untuk menyederhanakannya, kita akan melakukan rasionalisasi penyebut. Rasionalisasi penyebut adalah proses menghilangkan akar irasional dari penyebut suatu pecahan. Hal ini penting karena bentuk pecahan dengan penyebut irasional kurang praktis dalam perhitungan dan seringkali sulit diinterpretasikan.
Proses Rasionalisasi Penyebut
Untuk merasionalisasi penyebut 4√3, kita kalikan pecahan tersebut dengan bentuk 1 yang tepat, yaitu √3/√
3. Perhatikan langkah-langkah berikut:
- Kalikan pembilang dan penyebut dengan √3:
-
(15/(4√3))
- (√3/√3) = (15√3)/(4
- 3)
- Sederhanakan:
-
(15√3)/12 = (5√3)/4
Dengan demikian, bentuk paling sederhana dari 15/(4√3) adalah (5√3)/4.
Tabel Langkah Penyederhanaan
| Langkah | Ekspresi | Penjelasan | Hasil |
|---|---|---|---|
| 1 | 15/(4√3) | Ekspresi awal | 15/(4√3) |
| 2 | (15/(4√3)) – (√3/√3) | Rasionalisasi penyebut (dikalikan dengan √3/√3) | (15√3)/(4*3) |
| 3 | (15√3)/12 | Penyederhanaan penyebut | (15√3)/12 |
| 4 | (5√3)/4 | Penyederhanaan pecahan | (5√3)/4 |
Contoh Soal Serupa
Berikut contoh soal serupa dengan tingkat kesulitan yang berbeda:
- Sederhanakan ekspresi 6/(2√2). Penyelesaian: (6/(2√2)) – (√2/√2) = (6√2)/4 = (3√2)/2
- Sederhanakan ekspresi (10√5)/(5√2). Penyelesaian: (10√5)/(5√2) – (√2/√2) = (10√10)/10 = √10
Bentuk Sederhana dan Nilai Desimal: Bentuk Sederhana Dari 15 Per 4 Akar 3 Adalah
Berikut ini akan dijelaskan proses penyederhanaan ekspresi “15 per 4 akar 3” menjadi bentuk sederhana, perhitungan nilai desimalnya, dan perbandingan dengan nilai desimal ekspresi awal. Penjelasan ini akan mencakup tahapan penyederhanaan dengan ilustrasi visual deskriptif.
Penyederhanaan Ekspresi
Ekspresi “15 per 4 akar 3” dapat ditulis sebagai pecahan 15/(4√3). Untuk menyederhanakannya, kita akan menghilangkan akar pada penyebut dengan cara mengalikan pecahan tersebut dengan bentuk perkalian 1 yang tepat, yaitu (√3)/(√3).
Berikut tahapan penyederhanaannya:
- Kalikan pembilang dan penyebut dengan √3: [15/(4√3)] – (√3/√3) = (15√3)/(4*3)
- Sederhanakan penyebut: (15√3)/12
- Sederhanakan pecahan dengan membagi pembilang dan penyebut dengan 3: (5√3)/4
Jadi, bentuk sederhana dari 15/(4√3) adalah (5√3)/4.
Perhitungan Nilai Desimal
Setelah mendapatkan bentuk sederhana (5√3)/4, kita dapat menghitung nilai desimalnya. Nilai √3 sekitar 1.
732. Substitusikan nilai ini ke dalam bentuk sederhana:
(5
– 1.732) / 4 = 8.66 / 4 = 2.165
Dibulatkan hingga dua tempat desimal, nilai desimalnya adalah 2.17.
Perbandingan Nilai Desimal
Mari bandingkan nilai desimal bentuk sederhana dengan nilai desimal ekspresi awal 15/(4√3). Dengan menggunakan kalkulator, nilai desimal dari 15/(4√3) adalah sekitar 2.165.
Perbedaan nilai desimal antara ekspresi awal dan bentuk sederhananya sangat kecil, yaitu hanya sekitar 0.005. Perbedaan ini disebabkan oleh pembulatan nilai √3.
Perbedaan Bentuk Sederhana dan Nilai Desimal
Bentuk sederhana dari suatu ekspresi matematis adalah representasi ekspresi tersebut dalam bentuk yang paling ringkas dan efisien, biasanya dengan menghilangkan akar pada penyebut atau menyederhanakan pecahan. Nilai desimal, di sisi lain, adalah representasi numerik dari ekspresi tersebut dalam sistem bilangan desimal. Bentuk sederhana memudahkan manipulasi aljabar, sementara nilai desimal memberikan gambaran numerik langsung dari besaran tersebut.
Ilustrasi Visual Penyederhanaan
Bayangkan sebuah persegi panjang dengan luas 15. Kita membagi persegi panjang ini menjadi 4 bagian yang sama, masing-masing dengan luas 15/4. Kemudian, kita bayangkan setiap bagian tersebut dibagi lagi menjadi √3 bagian yang sama. Dengan mengalikan dengan √3/√3, kita mengubah representasi bagian-bagian tersebut, tetapi total luas tetap sama. Proses ini menghasilkan persegi panjang baru yang luasnya masih 15, tetapi terbagi menjadi bagian-bagian yang lebih mudah dihitung dan direpresentasikan dalam bentuk sederhana (5√3)/4.
Penerapan dalam Konteks Geometri
Bentuk sederhana dari ekspresi “15 per 4 akar 3”, setelah disederhanakan, memiliki aplikasi yang luas dalam berbagai perhitungan geometri, khususnya dalam menentukan panjang sisi atau tinggi segitiga. Pemahaman tentang penyederhanaan aljabar ini sangat penting untuk menyelesaikan masalah geometri dengan lebih efisien dan akurat.
Salah satu contoh penerapannya adalah dalam menghitung panjang sisi sebuah segitiga sama sisi.
Contoh Perhitungan Panjang Sisi Segitiga Sama Sisi
Bayangkan sebuah segitiga sama sisi dengan tinggi 15 cm. Kita dapat menggunakan rumus luas segitiga (½ x alas x tinggi) dan rumus tinggi segitiga sama sisi (√3/2 x sisi) untuk menemukan panjang sisinya. Dengan menggunakan bentuk sederhana dari “15 per 4 akar 3”, kita dapat menemukan panjang sisi segitiga ini dengan lebih mudah.
Berikut sketsa segitiga tersebut:
Segitiga ABC merupakan segitiga sama sisi. Titik D merupakan titik tengah sisi AB, sehingga AD = DB. CD merupakan tinggi segitiga, dengan panjang 15 cm. Sudut ACD = sudut BCD = 30 derajat. Sudut ADC = sudut BDC = 90 derajat.
Panjang sisi AC = BC = AB.
Langkah-langkah Penyelesaian
- Kita tahu tinggi segitiga sama sisi (h) dapat dirumuskan sebagai h = (√3/2) x sisi.
- Dalam kasus ini, h = 15 cm. Maka, 15 = (√3/2) x sisi.
- Untuk mencari panjang sisi, kita ubah rumus menjadi: sisi = (2 x 15) / √3 = 30 / √3.
- Rasionalisasi penyebut: sisi = (30 x √3) / (√3 x √3) = 30√3 / 3 = 10√3 cm.
- Ekspresi 15/(4√3) walaupun tidak secara langsung digunakan dalam perhitungan ini, prinsip rasionalisasi penyebut yang sama digunakan untuk menyederhanakan ekspresi tersebut dan bentuk penyederhanaan yang didapat dapat membantu dalam menyelesaikan masalah geometri yang lebih kompleks.
Contoh Masalah Geometri Lain
Prinsip yang sama, yaitu penggunaan rumus trigonometri dan aljabar untuk menyederhanakan ekspresi yang melibatkan akar, dapat diterapkan pada berbagai masalah geometri lainnya, misalnya menghitung luas segitiga sembarang jika diketahui panjang dua sisi dan sudut di antara keduanya (menggunakan rumus luas = ½ab sin C), atau menghitung panjang diagonal suatu persegi panjang jika diketahui panjang dan lebarnya (menggunakan teorema Pythagoras).
Analisis Kesalahan Umum
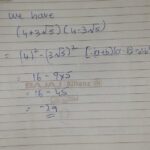
Penyederhanaan ekspresi yang melibatkan akar seringkali menimbulkan kesalahan. Pemahaman yang kurang tepat tentang aturan aljabar dan sifat-sifat akar dapat menyebabkan penyelesaian yang salah. Oleh karena itu, penting untuk mengidentifikasi kesalahan-kesalahan umum ini dan mempelajari cara mengatasinya agar dapat menghitung dengan akurat.
Kesalahan-kesalahan tersebut umumnya muncul karena kurangnya pemahaman mendalam mengenai operasi akar dan sifat-sifatnya, terutama dalam penggabungan operasi akar dengan operasi aljabar lainnya. Ketidaktelitian dalam langkah-langkah perhitungan juga sering menjadi penyebabnya.
Kesalahan dalam Mengoperasikan Akar, Bentuk sederhana dari 15 per 4 akar 3 adalah
Salah satu kesalahan umum adalah menganggap bahwa akar kuadrat dari penjumlahan dua bilangan sama dengan penjumlahan akar kuadrat masing-masing bilangan. Hal ini tidak benar. Sebagai contoh, √(4 + 9) ≠ √4 + √9. Sisi kiri sama dengan √13, sedangkan sisi kanan sama dengan 5. Kesalahan ini muncul karena pemahaman yang keliru tentang distributifitas operasi akar.
Kesalahan lain yang sering terjadi adalah kesalahan dalam merasionalkan penyebut yang mengandung akar. Misalnya, ketika merasionalkan 1/√2, beberapa orang mungkin langsung mengalikan dengan √2/√2, tetapi lupa untuk mengalikan seluruh pembilang dan penyebut. Ini akan menghasilkan hasil yang salah.
Contoh Soal dan Penyelesaian yang Benar
Berikut contoh soal yang menunjukkan kesalahan umum dan penyelesaian yang benar:
Soal: Sederhanakan ekspresi √(16 + 9)
Penyelesaian Salah: √(16 + 9) = √16 + √9 = 4 + 3 = 7
Penyelesaian Benar: √(16 + 9) = √25 = 5
Soal: Sederhanakan ekspresi 2/√3
Penyelesaian Salah: 2/√3 = 2√3/3√3 = 2√3/9 (salah karena hanya mengalikan √3 pada pembilang)
Penyelesaian Benar: 2/√3 = (2/√3)
– (√3/√3) = 2√3/3
Tabel Kesalahan Umum dan Cara Mengatasinya
| Kesalahan | Penjelasan | Contoh | Cara Mengatasi |
|---|---|---|---|
| √(a + b) = √a + √b | Operasi akar tidak distributif terhadap penjumlahan. | √(4 + 9) ≠ √4 + √9 | Hitung nilai dalam tanda kurung terlebih dahulu sebelum mengambil akar. |
| Kesalahan dalam merasionalkan penyebut | Tidak mengalikan seluruh pembilang dan penyebut dengan faktor rasionalisasi. | 2/√3 = 2√3/3√3 = 2√3/9 | Pastikan mengalikan seluruh pembilang dan penyebut dengan faktor rasionalisasi. |
| Kesalahan dalam menyederhanakan akar | Tidak menyederhanakan akar semaksimal mungkin. | √12 = 2√3 | Faktorkan bilangan di dalam akar dan keluarkan faktor yang merupakan kuadrat sempurna. |
| Mengabaikan tanda negatif pada akar | Mengabaikan bahwa akar kuadrat dari bilangan positif memiliki dua nilai, positif dan negatif. | x² = 9, maka x = ±3 | Perhatikan tanda positif dan negatif pada akar kuadrat. |
Tips Menghindari Kesalahan
Untuk menghindari kesalahan, penting untuk memahami sifat-sifat akar dan aturan aljabar dengan baik. Selalu perhatikan langkah-langkah perhitungan dan periksa kembali hasil akhir. Berlatih mengerjakan soal-soal yang beragam dapat meningkatkan pemahaman dan keakuratan dalam menyederhanakan ekspresi yang melibatkan akar.
Terakhir
Menyederhanakan ekspresi matematika seperti “15 per 4 akar 3” tidak hanya tentang mendapatkan jawaban akhir, tetapi juga tentang memahami proses dan konsep yang mendasarinya. Rasionalisasi penyebut merupakan teknik penting yang mempermudah perhitungan dan pemahaman dalam berbagai aplikasi matematika, termasuk geometri. Dengan memahami langkah-langkah penyederhanaan dan kesalahan umum yang mungkin terjadi, kita dapat meningkatkan kemampuan kita dalam menyelesaikan masalah matematika dengan lebih akurat dan efisien.
Semoga penjelasan di atas memberikan pemahaman yang lebih baik tentang penyederhanaan ekspresi aljabar yang melibatkan akar.