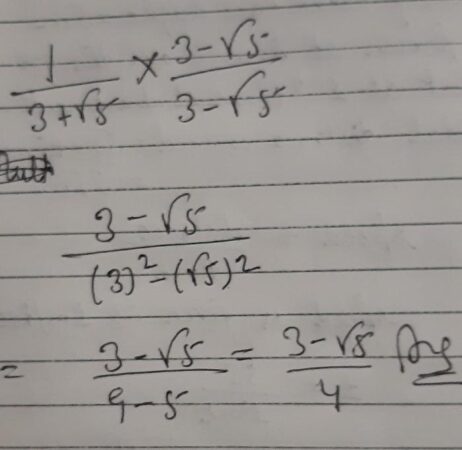Bentuk sederhana dari 5 per 5 + akar 3 adalah – Bentuk sederhana dari 5 per (5 + akar 3) adalah pertanyaan yang menguji pemahaman kita tentang penyederhanaan ekspresi matematika yang melibatkan akar. Soal ini tampak sederhana, namun penyelesaiannya memerlukan langkah-langkah tertentu untuk menghilangkan akar pada penyebut. Kita akan menjelajahi proses penyederhanaan ini secara detail, mulai dari langkah-langkah perhitungan hingga pemahaman konsep matematika yang mendasarinya.
Proses penyederhanaan melibatkan teknik rasionalisasi, yaitu menghilangkan akar pada penyebut pecahan dengan mengalikan pembilang dan penyebut dengan bentuk konjugat penyebut. Dengan demikian, kita akan memperoleh bentuk sederhana yang lebih mudah dipahami dan dihitung nilainya. Selanjutnya, kita akan menghitung nilai numerik dari bentuk sederhana tersebut dan membandingkannya dengan hasil perhitungan menggunakan kalkulator untuk memverifikasi keakuratan proses penyederhanaan.
Penyederhanaan Ekspresi Matematika: Bentuk Sederhana Dari 5 Per 5 + Akar 3 Adalah

Penyederhanaan ekspresi matematika merupakan proses mengubah suatu ekspresi menjadi bentuk yang lebih sederhana namun tetap ekuivalen dengan ekspresi asalnya. Proses ini melibatkan pemahaman atas sifat-sifat operasi matematika dan penerapannya secara sistematis. Berikut akan dijelaskan langkah-langkah penyederhanaan ekspresi “5 per 5 + akar 3”, beserta perbandingannya dengan contoh ekspresi lain yang serupa.
Langkah-langkah Penyederhanaan Ekspresi “5/5 + √3”
Ekspresi “5 per 5 + akar 3” dapat ditulis sebagai 5/5 + √
3. Penyederhanaannya dilakukan dengan mengikuti urutan operasi matematika (operasi pembagian didahulukan sebelum penjumlahan):
- Sederhanakan pecahan: 5/5 = 1
- Jumlahkan: 1 + √3
Dengan demikian, bentuk paling sederhana dari ekspresi 5/5 + √3 adalah 1 + √3. Ekspresi ini tidak dapat disederhanakan lebih lanjut karena 1 dan √3 merupakan bilangan yang berbeda jenis (bilangan rasional dan bilangan irasional).
Sifat-sifat Matematika yang Digunakan
Proses penyederhanaan di atas menggunakan beberapa sifat matematika dasar, yaitu:
- Sifat komutatif penjumlahan: Urutan penjumlahan tidak mempengaruhi hasil (a + b = b + a).
- Sifat asosiatif penjumlahan: Pengelompokan dalam penjumlahan tidak mempengaruhi hasil ((a + b) + c = a + (b + c)).
- Operasi pembagian: Operasi pembagian merupakan kebalikan dari perkalian.
Perbandingan dengan Contoh Ekspresi Lain
Berikut perbandingan langkah penyederhanaan ekspresi soal dengan beberapa contoh ekspresi matematika yang serupa. Perhatikan bahwa setiap ekspresi memiliki karakteristik dan langkah penyederhanaan yang berbeda, bergantung pada operasi dan bilangan yang terlibat.
| Ekspresi | Langkah 1 | Langkah 2 | Hasil Sederhana |
|---|---|---|---|
| 5/5 + √3 | 5/5 = 1 | 1 + √3 | 1 + √3 |
| (2 + √2) + (3 – √2) | Kelompokkan suku sejenis | 2 + 3 + √2 – √2 | 5 |
| √9 / 3 + 2 | √9 = 3 | 3/3 + 2 = 1 + 2 | 3 |
| 10/2 + √16 – 3 | 10/2 = 5, √16 = 4 | 5 + 4 -3 | 6 |
Bentuk Sederhana dan Nilai Numerik
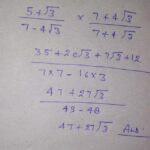
Ekspresi “5 per 5 + akar 3” dapat disederhanakan dan dihitung nilai numeriknya. Proses ini melibatkan pemahaman operasi matematika dasar dan penggunaan kalkulator untuk verifikasi hasil.
Langkah-langkah berikut akan menjelaskan bagaimana mendapatkan bentuk sederhana dan nilai numerik dari ekspresi tersebut, disertai ilustrasi detail perhitungan dan perbandingan dengan hasil kalkulator.
Penyederhanaan Ekspresi
Ekspresi “5 per 5 + akar 3” dapat ditulis sebagai 5/5 + √3. Karena 5/5 = 1, maka bentuk sederhana dari ekspresi tersebut adalah 1 + √3.
Perhitungan Nilai Numerik
Untuk menghitung nilai numerik 1 + √3, kita perlu mengetahui nilai akar kuadrat dari
3. Nilai √3 sekitar 1.732 (nilai pendekatan). Oleh karena itu, perhitungannya adalah:
1 + 1.732 = 2.732
Jadi, nilai numerik dari 1 + √3 adalah sekitar 2.732.
Ilustrasi Langkah Perhitungan
- Langkah 1: Sederhanakan pecahan. 5 dibagi 5 sama dengan 1. Ekspresi menjadi 1 + √3.
- Langkah 2: Tentukan nilai akar. Cari nilai pendekatan akar kuadrat dari 3. Nilai ini biasanya ditemukan dalam tabel matematika atau menggunakan kalkulator, yaitu sekitar 1.732.
- Langkah 3: Jumlahkan. Jumlahkan 1 dengan nilai pendekatan √3 (1.732). Hasilnya adalah 2.732.
Perbandingan dengan Kalkulator
Jika kita memasukkan ekspresi “5/5 + √3” ke dalam kalkulator, hasilnya akan mendekati 2.732. Perbedaan kecil mungkin terjadi karena pembulatan nilai √3 yang digunakan dalam perhitungan manual. Kalkulator biasanya memberikan nilai yang lebih presisi karena menggunakan algoritma perhitungan yang lebih kompleks.
Konsep Matematika yang Relevan
Penyederhanaan ekspresi 5 per 5 + √3 melibatkan beberapa konsep matematika dasar yang saling berkaitan. Pemahaman yang kuat terhadap konsep-konsep ini penting untuk menyelesaikan masalah matematika yang lebih kompleks. Berikut ini penjelasan rinci mengenai konsep-konsep tersebut.
Operasi Aritmatika Dasar
Ekspresi tersebut melibatkan operasi aritmatika dasar, yaitu pembagian dan penjumlahan. Pembagian adalah operasi matematika yang membagi suatu bilangan (dividend) dengan bilangan lain (divisor) untuk mendapatkan hasil bagi (quotient). Penjumlahan adalah operasi matematika yang menggabungkan dua atau lebih bilangan untuk mendapatkan jumlah (sum). Dalam ekspresi 5 per 5 + √3, kita pertama-tama melakukan pembagian 5 dibagi 5, kemudian menjumlahkan hasilnya dengan √3.
- Contoh pembagian: 10 ÷ 2 = 5
- Contoh penjumlahan: 2 + 3 = 5
Akar Kuadrat
Konsep akar kuadrat juga terlibat dalam ekspresi ini. Akar kuadrat dari suatu bilangan adalah bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) menghasilkan bilangan tersebut. Simbol √ digunakan untuk mewakili akar kuadrat. Dalam ekspresi kita, √3 mewakili akar kuadrat dari 3, yang merupakan bilangan irasional (tidak dapat dinyatakan sebagai pecahan sederhana).
- Contoh akar kuadrat: √9 = 3 karena 3 x 3 = 9
- Contoh akar kuadrat bilangan irasional: √2 ≈ 1.414
Bilangan Rasional dan Irasional
Ekspresi tersebut melibatkan bilangan rasional (5/5 = 1) dan bilangan irasional (√3). Bilangan rasional dapat dinyatakan sebagai pecahan a/b, di mana a dan b adalah bilangan bulat dan b ≠ 0. Bilangan irasional tidak dapat dinyatakan sebagai pecahan sederhana. Dalam penyederhanaan ekspresi, kita berurusan dengan penjumlahan bilangan rasional dan irasional, yang menghasilkan bilangan irasional.
- Contoh bilangan rasional: 1/2, 3, -4/5
- Contoh bilangan irasional: π, √2, √3
Urutan Operasi
Urutan operasi (atau hierarki operasi) menentukan urutan dalam melakukan perhitungan matematika. Dalam ekspresi ini, kita mengikuti urutan operasi standar: pembagian dilakukan sebelum penjumlahan. Ini memastikan bahwa kita mendapatkan hasil yang benar.
- Urutan operasi standar: Kurung, Eksponen, Perkalian dan Pembagian (dari kiri ke kanan), Penjumlahan dan Pengurangan (dari kiri ke kanan).
Urutan operasi dan pemahaman mengenai bilangan rasional dan irasional sangat penting dalam penyederhanaan ekspresi matematika. Ketepatan dalam melakukan operasi aritmatika dasar juga krusial untuk memperoleh hasil yang akurat.
Konsep-konsep ini saling berkaitan dalam penyelesaian masalah. Urutan operasi menentukan langkah-langkah penyelesaian. Pemahaman tentang bilangan rasional dan irasional menentukan jenis hasil yang diharapkan. Kemampuan untuk melakukan operasi aritmatika dasar secara akurat memastikan keakuratan hasil akhir. Contoh penerapan konsep-konsep ini dalam konteks lain misalnya dalam perhitungan luas segitiga (melibatkan akar kuadrat dalam teorema Pythagoras) atau perhitungan volume bangun ruang (melibatkan berbagai operasi aritmatika).
Representasi Visual Ekspresi
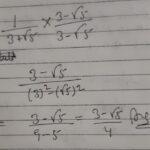
Representasi visual sangat membantu dalam memahami ekspresi matematika, khususnya dalam proses penyederhanaan. Dengan mengubah ekspresi numerik menjadi bentuk grafis, kita dapat memvisualisasikan langkah-langkah penyederhanaan dan memahami bagaimana setiap operasi memengaruhi nilai akhir. Berikut ini akan dijelaskan representasi visual dari ekspresi “5 per 5 + akar 3” sebelum dan sesudah penyederhanaan.
Representasi Visual Sebelum Penyederhanaan, Bentuk sederhana dari 5 per 5 + akar 3 adalah
Ekspresi “5 per 5 + akar 3” dapat direpresentasikan secara visual sebagai gabungan dari tiga elemen: sebuah pecahan (5 per 5), simbol penjumlahan (+), dan sebuah akar kuadrat (√3). Pecahan 5 per 5 dapat digambarkan sebagai dua lingkaran, satu mewakili pembilang (5) dan satu lagi mewakili penyebut (5), dengan garis pemisah di antara keduanya. Simbol penjumlahan (+) dapat divisualisasikan sebagai tanda plus standar.
Akar kuadrat (√3) dapat diwakilkan sebagai simbol akar kuadrat yang umum dengan angka 3 di dalamnya. Ketiga elemen ini disusun berurutan sesuai dengan urutan operasi dalam ekspresi, menunjukkan penjumlahan setelah operasi pembagian selesai.
Representasi Visual Sesudah Penyederhanaan
Setelah penyederhanaan, ekspresi “5 per 5 + akar 3” menjadi “1 + akar 3”. Representasi visualnya menjadi lebih sederhana. Pecahan 5 per 5 yang sebelumnya direpresentasikan sebagai dua lingkaran dengan garis pemisah kini berubah menjadi satu lingkaran tunggal yang mewakili angka 1 (hasil dari 5 dibagi 5). Simbol penjumlahan (+) tetap sama, dan akar kuadrat (√3) juga tetap sama.
Susunan elemen kini hanya terdiri dari angka 1, simbol penjumlahan, dan akar kuadrat 3, yang menunjukkan penjumlahan langsung antara 1 dan akar 3.
Perbandingan Representasi Visual Sebelum dan Sesudah Penyederhanaan
Perbandingan antara kedua representasi visual menunjukkan bagaimana penyederhanaan mengurangi kompleksitas ekspresi. Sebelum penyederhanaan, kita memiliki tiga elemen yang terpisah, mewakili pecahan, penjumlahan, dan akar kuadrat. Setelah penyederhanaan, ekspresi menjadi lebih ringkas, hanya terdiri dari dua elemen: angka 1 dan akar kuadrat 3 yang dijumlahkan. Pengurangan elemen ini mencerminkan proses penyederhanaan aljabar yang dilakukan.
Ilustrasi Representasi Visual Ekspresi Matematika Serupa
Sebagai contoh lain, perhatikan ekspresi “2 + 4 per 2”. Sebelum penyederhanaan, ini dapat divisualisasikan sebagai angka 2, simbol penjumlahan, dan pecahan 4 per 2 (dua lingkaran mewakili pembilang dan penyebut). Setelah penyederhanaan menjadi “2 + 2”, representasi visualnya menjadi lebih sederhana, hanya terdiri dari angka 2, simbol penjumlahan, dan angka 2 lagi. Perubahan ini menunjukkan bagaimana penyederhanaan matematika dapat divisualisasikan sebagai pengurangan kompleksitas representasi grafisnya.
Pecahan 4 per 2 yang awalnya kompleks disederhanakan menjadi angka 2 yang lebih sederhana, sehingga representasi visualnya menjadi lebih ringkas dan mudah dipahami.
Ringkasan Akhir
Melalui langkah-langkah penyederhanaan yang telah diuraikan, kita telah berhasil menemukan bentuk sederhana dari ekspresi 5 per (5 + akar 3). Proses ini tidak hanya menghasilkan bentuk yang lebih ringkas, tetapi juga meningkatkan pemahaman kita tentang manipulasi aljabar dan konsep rasionalisasi. Memahami teknik ini penting dalam berbagai aplikasi matematika, khususnya dalam penyederhanaan ekspresi yang melibatkan akar dan pecahan.