Contoh soal barisan geometri merupakan pintu gerbang untuk memahami konsep matematika yang menarik ini. Barisan geometri, dengan polanya yang unik dan rumus-rumusnya yang elegan, seringkali muncul dalam berbagai konteks, dari perhitungan bunga majemuk hingga pertumbuhan populasi. Memahami barisan geometri tidak hanya penting untuk akademis, tetapi juga untuk mengaplikasikannya dalam kehidupan sehari-hari.
Dalam pembahasan ini, kita akan menjelajahi berbagai aspek barisan geometri, mulai dari definisi dan rumus dasar hingga penyelesaian soal-soal yang lebih kompleks. Kita akan melihat bagaimana membedakan barisan geometri dari barisan aritmatika, mengerjakan contoh soal dengan tingkat kesulitan yang bervariasi, dan mengamati penerapannya dalam berbagai situasi nyata. Siapkan diri Anda untuk menjelajahi dunia bilangan yang menakjubkan ini!
Pengertian Barisan Geometri
Barisan geometri merupakan suatu barisan bilangan yang memiliki pola tetap berupa perkalian atau pembagian dengan suatu bilangan konstan yang disebut rasio (r). Setiap suku berikutnya diperoleh dengan mengalikan suku sebelumnya dengan rasio tersebut. Berbeda dengan barisan aritmatika yang memiliki selisih tetap antar suku, barisan geometri memiliki rasio tetap. Pemahaman tentang barisan geometri sangat penting dalam berbagai aplikasi matematika dan kehidupan sehari-hari, seperti pertumbuhan populasi, bunga majemuk, dan perkembangbiakan bakteri.
Sebagai contoh, barisan 2, 6, 18, 54, … merupakan barisan geometri karena setiap suku diperoleh dengan mengalikan suku sebelumnya dengan 3 (rasio = 3). Perhatikan bahwa rasio (r) selalu konstan pada barisan geometri.
Perbedaan Barisan Geometri dan Barisan Aritmatika
Berikut tabel yang membandingkan barisan geometri dan barisan aritmatika, menyoroti perbedaan kunci di antara keduanya:
| Nama Barisan | Rumus Suku ke-n | Rumus Jumlah n Suku Pertama | Contoh |
|---|---|---|---|
| Barisan Aritmatika | an = a1 + (n-1)b(a1 = suku pertama, b = beda) |
Sn = n/2 (2a1 + (n-1)b) |
3, 7, 11, 15, … (beda = 4) |
| Barisan Geometri | an = a1(a 1 = suku pertama, r = rasio) |
Sn = a 1(1 – r n) / (1 – r)(untuk r ≠ 1) |
2, 6, 18, 54, … (rasio = 3) |
Ilustrasi Perbedaan Barisan Geometri dan Barisan Aritmatika
Bayangkan dua skenario: Skenario pertama menggambarkan pertumbuhan populasi kelinci yang berkembang biak secara eksponensial (barisan geometri). Misalnya, jika sepasang kelinci menghasilkan 2 pasang kelinci setiap bulan, maka populasi akan mengikuti pola 2, 4, 8, 16, 32, dan seterusnya.
Perhatikan bahwa pertumbuhannya semakin cepat setiap bulannya, sesuai dengan sifat barisan geometri. Skenario kedua menggambarkan pertumbuhan tinggi tanaman yang bertambah secara konstan setiap minggu (barisan aritmatika). Misalnya, jika tanaman tumbuh 2 cm setiap minggu, maka pertumbuhannya akan mengikuti pola 2, 4, 6, 8, 10, dan seterusnya. Perhatikan bahwa pertumbuhannya konstan dan linear, sesuai dengan sifat barisan aritmatika.
Perbedaan mendasar terletak pada pola pertumbuhan: eksponensial pada barisan geometri dan linear pada barisan aritmatika.
Ciri-Ciri Utama Barisan Geometri, Contoh soal barisan geometri
Ciri utama yang membedakan barisan geometri dari jenis barisan lainnya adalah rasio konstan antara dua suku berurutan. Rasio ini diperoleh dengan membagi suatu suku dengan suku sebelumnya. Jika rasio konstan, maka barisan tersebut merupakan barisan geometri. Ciri lainnya adalah pola pertumbuhan atau penyusutan yang eksponensial, bukan linear seperti pada barisan aritmatika.
Contoh Soal Cerita Barisan Geometri
Sebuah bakteri membelah diri menjadi dua setiap 20 menit. Jika awalnya terdapat 1 bakteri, berapa banyak bakteri yang ada setelah 1 jam (60 menit)?
Penyelesaian: Karena bakteri membelah diri setiap 20 menit, maka dalam 1 jam (60 menit) terjadi 3 kali pembelahan (60 menit / 20 menit/pembelahan = 3 pembelahan). Jadi, pola pertumbuhan bakteri mengikuti barisan geometri dengan a 1 = 1 dan r = 2. Jumlah bakteri setelah 1 jam adalah a 4 = a 1
– r (4-1) = 1
– 2 3 = 8 bakteri.
Rumus-Rumus Penting Barisan Geometri

Barisan geometri merupakan barisan bilangan yang memiliki rasio tetap antara dua suku berurutan. Memahami rumus-rumus barisan geometri sangat penting untuk menyelesaikan berbagai permasalahan yang berkaitan dengan pertumbuhan eksponensial atau peluruhan. Berikut ini akan dijelaskan rumus-rumus penting beserta contoh penerapannya.
Rumus Suku ke-n Barisan Geometri
Rumus suku ke-n barisan geometri digunakan untuk menentukan nilai suku pada urutan tertentu dalam barisan tersebut. Rumusnya adalah:
Un = a . r n-1
di mana:
- U n = suku ke-n
- a = suku pertama
- r = rasio (perbandingan antara dua suku berurutan)
- n = urutan suku
Contoh: Tentukan suku ke-5 dari barisan geometri 2, 6, 18, …
Langkah-langkah penyelesaian:
- Tentukan suku pertama (a): a = 2
- Tentukan rasio (r): r = 6/2 = 3
- Tentukan urutan suku (n): n = 5
- Substitusikan nilai a, r, dan n ke dalam rumus: U5 = 2 . 3 5-1 = 2 . 3 4 = 2 . 81 = 162
Jadi, suku ke-5 dari barisan geometri tersebut adalah 162.
Rumus Jumlah n Suku Pertama Barisan Geometri
Rumus ini digunakan untuk menghitung jumlah dari sejumlah suku pertama dalam barisan geometri. Rumusnya terbagi menjadi dua, bergantung pada nilai rasio (r).
Jika r ≠ 1, rumusnya adalah:
Sn = a(r n
1) / (r – 1)
Jika r = 1, rumusnya adalah:
Sn = n . a
di mana:
- S n = jumlah n suku pertama
- a = suku pertama
- r = rasio
- n = banyaknya suku
Contoh 1 (r ≠ 1): Hitung jumlah 4 suku pertama dari barisan geometri 3, 6, 12, 24, …
- Tentukan suku pertama (a): a = 3
- Tentukan rasio (r): r = 6/3 = 2
- Tentukan banyaknya suku (n): n = 4
- Substitusikan nilai a, r, dan n ke dalam rumus: S4 = 3(2 4
1) / (2 – 1) = 3(16 – 1) / 1 = 45
Jadi, jumlah 4 suku pertama adalah 45.
Contoh 2 (r = 1): Hitung jumlah 5 suku pertama dari barisan geometri 5, 5, 5, 5, 5, …
- Karena r = 1, gunakan rumus Sn = n . a
- Tentukan suku pertama (a): a = 5
- Tentukan banyaknya suku (n): n = 5
- Substitusikan nilai a dan n ke dalam rumus: S 5 = 5 . 5 = 25
Jadi, jumlah 5 suku pertama adalah 25.
Langkah-Langkah Sistematis Menyelesaikan Soal Jumlah n Suku Pertama Barisan Geometri
Untuk menyelesaikan soal yang melibatkan rumus jumlah n suku pertama barisan geometri, ikuti langkah-langkah berikut:
- Identifikasi apakah barisan tersebut merupakan barisan geometri. Periksa apakah rasio antara dua suku berurutan konstan.
- Tentukan nilai suku pertama (a) dan rasio (r).
- Tentukan nilai n (banyaknya suku yang akan dijumlahkan).
- Pilih rumus yang tepat (r = 1 atau r ≠ 1).
- Substitusikan nilai a, r, dan n ke dalam rumus yang telah dipilih.
- Hitung hasilnya.
Jenis-Jenis Soal Barisan Geometri
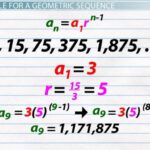
Barisan geometri merupakan barisan bilangan yang memiliki rasio tetap antara setiap suku yang berurutan. Pemahaman tentang barisan geometri sangat penting, karena konsep ini banyak diaplikasikan dalam berbagai bidang, mulai dari matematika keuangan hingga pertumbuhan populasi. Berbagai tipe soal dapat dijumpai, dan memahami cara penyelesaiannya merupakan kunci untuk menguasai materi ini.
Berikut ini akan dijelaskan beberapa tipe soal barisan geometri yang sering muncul, disertai contoh soal dan penyelesaiannya. Penjelasan ini akan mencakup soal mencari suku ke-n, jumlah n suku pertama, rasio, dan suku pertama, serta contoh soal cerita dengan tingkat kesulitan yang bervariasi.
Mencari Suku ke-n
Mencari suku ke-n (a n) dari suatu barisan geometri membutuhkan rumus umum suku ke-n barisan geometri, yaitu a n = a 1
– r n-1, di mana a 1 adalah suku pertama, r adalah rasio, dan n adalah nomor suku yang dicari. Berikut contohnya:
Contoh Soal: Suatu barisan geometri memiliki suku pertama 3 dan rasio 2. Tentukan suku ke-5 barisan tersebut.
Penyelesaian:
Diketahui: a 1 = 3, r = 2, n = 5
a n = a 1
– r n-1
a 5 = 3
– 2 5-1 = 3
– 2 4 = 3
– 16 = 48
Jadi, suku ke-5 barisan geometri tersebut adalah 48.
Mencari Jumlah n Suku Pertama
Mencari jumlah n suku pertama (S n) dari barisan geometri menggunakan rumus S n = a 1(r n
-1) / (r – 1) jika r > 1, atau S n = a 1(1 – r n) / (1 – r) jika r < 1. Rumus ini sangat berguna untuk menghitung total akumulasi suatu besaran yang mengikuti pola geometri.
Contoh Soal: Tentukan jumlah 6 suku pertama dari barisan geometri 2, 6, 18, …
Penyelesaian:
Diketahui: a 1 = 2, r = 3, n = 6
Karena r > 1, kita gunakan rumus S n = a 1(r n
-1) / (r – 1)
S 6 = 2(3 6
-1) / (3 – 1) = 2(729 – 1) / 2 = 728
Jadi, jumlah 6 suku pertama barisan geometri tersebut adalah 728.
Mencari Rasio dan Suku Pertama
Menentukan rasio dan suku pertama suatu barisan geometri dapat dilakukan jika beberapa suku barisan tersebut diketahui. Rasio dapat dicari dengan membagi suatu suku dengan suku sebelumnya. Suku pertama adalah suku pertama barisan tersebut.
Contoh Soal: Tentukan rasio dan suku pertama dari barisan geometri 4, 12, 36, 108, …
Penyelesaian:
Rasio (r) = 12/4 = 3
Suku pertama (a 1) = 4
Jadi, rasio barisan geometri tersebut adalah 3 dan suku pertamanya adalah 4.
Contoh Soal Cerita Barisan Geometri
Sebuah bola dijatuhkan dari ketinggian 10 meter. Setiap kali memantul, bola mencapai ketinggian 2/3 dari ketinggian sebelumnya. Berapa total jarak yang ditempuh bola hingga berhenti?
Penyelesaian:
Situasi masalah menggambarkan barisan geometri. Jarak turun pertama adalah 10 meter. Jarak pantulan pertama adalah 10
– (2/3) meter. Jarak pantulan kedua adalah 10
– (2/3) 2 meter, dan seterusnya. Total jarak adalah penjumlahan dari jarak turun dan jarak pantulan yang membentuk deret geometri tak hingga dengan rasio |r| < 1. Rumus deret geometri tak hingga konvergen adalah S∞ = a 1 / (1 – r), dengan a 1 = 10 dan r = 2/3.
Namun, perlu diingat bahwa ini adalah total jarak
-turun*. Untuk total jarak, kita perlu menggandakan hasil ini (kecuali jarak turun pertama), kemudian menambahkan jarak turun pertama. Perhitungannya:
S ∞ = 10 / (1 – 2/3) = 30 meter (total jarak turun)
Total jarak = 10 + 2
– 30 – 10 = 50 meter
Jadi, total jarak yang ditempuh bola hingga berhenti adalah 50 meter.
Contoh Soal Tingkat Kesulitan Berbeda
Berikut beberapa contoh soal dengan tingkat kesulitan berbeda:
- Mudah: Tentukan suku ke-4 dari barisan geometri 1, 3, 9, … (Jawaban: 27)
- Sedang: Jumlah tiga suku pertama barisan geometri adalah 26 dan rasio adalah
3. Tentukan suku pertama. (Jawaban
2)
- Sulit: Suatu bakteri membelah diri menjadi dua setiap 20 menit. Jika awalnya terdapat 5 bakteri, berapa banyak bakteri setelah 2 jam? (Jawaban: 320 bakteri)
Penerapan Barisan Geometri dalam Kehidupan Sehari-hari

Barisan geometri, dengan pola perkalian konstan antara suku-sukunya, memiliki penerapan luas dalam berbagai aspek kehidupan. Konsep ini tidak hanya terbatas pada matematika abstrak, tetapi juga berperan penting dalam memahami dan memprediksi fenomena di dunia nyata, mulai dari pertumbuhan ekonomi hingga perkembangan populasi.
Contoh Penerapan Barisan Geometri dalam Kehidupan Nyata
Berikut beberapa contoh konkret penerapan barisan geometri dalam kehidupan sehari-hari:
- Perkembangbiakan Bakteri: Bakteri tertentu berkembang biak dengan membelah diri. Jika satu bakteri membelah diri menjadi dua setiap jam, maka jumlah bakteri akan membentuk barisan geometri: 1, 2, 4, 8, 16, dan seterusnya.
- Penurunan Nilai Aset: Nilai aset seperti mobil atau komputer cenderung mengalami depresiasi (penurunan nilai) secara geometrik setiap tahunnya. Misalnya, mobil yang bernilai Rp 500.000.000,- mungkin berkurang nilainya sebesar 10% setiap tahun, sehingga membentuk barisan geometri yang menurun.
- Virus yang Menular: Penyebaran virus tertentu dapat dimodelkan menggunakan barisan geometri, terutama pada tahap awal penyebaran ketika setiap individu yang terinfeksi menularkan virus ke sejumlah orang lain. Tentu saja, model ini menjadi lebih kompleks seiring waktu karena faktor-faktor lain seperti imunitas dan tindakan pencegahan.
Penggunaan Barisan Geometri dalam Bidang Ekonomi
Barisan geometri memainkan peran krusial dalam analisis ekonomi, khususnya dalam perhitungan pertumbuhan ekonomi dan investasi. Pertumbuhan ekonomi yang stabil seringkali dimodelkan sebagai barisan geometri, di mana pertumbuhan ekonomi tahunan dikalikan dengan angka pertumbuhan sebelumnya untuk memprediksi pertumbuhan di tahun berikutnya. Investasi, terutama yang berkaitan dengan bunga majemuk, juga sangat bergantung pada konsep barisan geometri.
Perhitungan Bunga Majemuk
Bunga majemuk merupakan contoh klasik penerapan barisan geometri. Pada bunga majemuk, bunga yang diperoleh di setiap periode ditambahkan ke pokok, sehingga bunga di periode berikutnya dihitung berdasarkan jumlah pokok ditambah bunga sebelumnya. Rumus untuk menghitung jumlah akhir (A) setelah n periode adalah: A = P (1 + r)^n, di mana P adalah pokok, r adalah suku bunga per periode, dan n adalah jumlah periode.
Rumus ini menunjukkan pola barisan geometri dengan rasio (1 + r).
Penerapan Barisan Geometri dalam Perhitungan Pertumbuhan Populasi
Pertumbuhan populasi, baik manusia, hewan, maupun tumbuhan, dapat dimodelkan menggunakan barisan geometri, terutama jika pertumbuhan tersebut konstan dan tidak dipengaruhi faktor-faktor pembatas seperti ketersediaan makanan atau penyakit. Model ini memberikan perkiraan sederhana namun berguna untuk memahami tren pertumbuhan populasi dalam jangka pendek.
Contoh Soal Cerita: Pertumbuhan Populasi Bakteri
Sebuah koloni bakteri awalnya berjumlah 1000 sel. Jika jumlah bakteri tersebut berlipat ganda setiap 30 menit, berapakah jumlah bakteri setelah 2 jam?
Penyelesaian: Karena bakteri berlipat ganda setiap 30 menit, dan 2 jam sama dengan 4 periode 30 menit, maka kita dapat menggunakan rumus barisan geometri: Jumlah bakteri = 1000 x 2^4 = 16000. Jadi, setelah 2 jam, jumlah bakteri akan menjadi 16.000 sel.
Penyelesaian Soal Barisan Geometri yang Lebih Kompleks
Setelah memahami konsep dasar barisan geometri, kita akan menghadapi soal-soal yang lebih menantang. Soal-soal ini seringkali melibatkan penerapan konsep barisan geometri dalam konteks persamaan kuadrat, sistem persamaan, limit, dan deret geometri tak hingga. Pemahaman yang kuat tentang sifat-sifat barisan geometri dan kemampuan aljabar yang baik akan sangat membantu dalam menyelesaikannya.
Barisan Geometri dan Persamaan Kuadrat
Beberapa soal barisan geometri membutuhkan penyelesaian persamaan kuadrat untuk menemukan nilai suku-suku yang belum diketahui. Misalnya, jika diketahui suku ke-2 dan suku ke-5 suatu barisan geometri, kita dapat membentuk dua persamaan dan menyelesaikannya menggunakan metode substitusi atau eliminasi untuk mencari rasio dan suku pertama.
Contoh: Diketahui suku kedua (a 2) suatu barisan geometri adalah 6 dan suku kelima (a 5) adalah 162. Tentukan suku pertama (a 1) dan rasio (r) barisan tersebut. Penyelesaiannya melibatkan pembentukan persamaan a 2 = a 1r = 6 dan a 5 = a 1r 4 = 162. Dari sini, kita dapat memperoleh persamaan kuadrat untuk r dan selanjutnya menghitung a 1.
Barisan Geometri dan Sistem Persamaan
Soal-soal yang lebih kompleks mungkin melibatkan beberapa barisan geometri sekaligus, sehingga membutuhkan penyelesaian sistem persamaan. Setiap barisan akan menghasilkan satu atau lebih persamaan, dan sistem persamaan tersebut harus diselesaikan secara simultan untuk menemukan nilai-nilai yang dibutuhkan.
Contoh: Dua barisan geometri memiliki suku pertama yang sama. Suku kedua barisan pertama adalah 12 dan suku ketiga barisan kedua adalah 27. Jika rasio barisan pertama adalah dua kali rasio barisan kedua, tentukan suku pertama dan rasio kedua barisan tersebut. Penyelesaiannya melibatkan pembentukan sistem persamaan yang terdiri dari persamaan-persamaan yang melibatkan suku-suku kedua dan ketiga dari kedua barisan dan relasi antara rasio kedua barisan.
Barisan Geometri dan Konsep Limit
Konsep limit seringkali muncul dalam konteks deret geometri tak hingga. Limit suatu deret geometri tak hingga menunjukan nilai pendekatan jumlah suku-suku deret tersebut ketika jumlah suku mendekati tak hingga. Nilai limit ini hanya ada jika nilai mutlak rasio kurang dari 1.
Contoh: Tentukan jumlah tak hingga dari deret geometri 1 + 1/2 + 1/4 + 1/8 + … . Penyelesaiannya menggunakan rumus jumlah deret geometri tak hingga, yaitu S = a 1/(1-r), dimana a 1 adalah suku pertama dan r adalah rasio. Dalam contoh ini, a 1 = 1 dan r = 1/2, sehingga jumlah tak hingga deret tersebut adalah 2.
Barisan Geometri dan Deret Geometri Tak Hingga
Deret geometri tak hingga merupakan penjumlahan dari semua suku dalam suatu barisan geometri. Jumlah deret geometri tak hingga hanya konvergen (mempunyai nilai tertentu) jika nilai mutlak rasio kurang dari 1. Jika nilai mutlak rasio lebih besar atau sama dengan 1, maka deret tersebut divergen (jumlahnya tidak terbatas).
Contoh: Analisis konvergensi dan tentukan jumlah deret geometri 3 + 6 + 12 + 24 + … . Dalam contoh ini, rasio (r) adalah 2, yang nilai mutlaknya lebih besar dari 1, sehingga deret tersebut divergen dan tidak memiliki jumlah yang terdefinisi.
Contoh Soal Barisan Geometri yang Memerlukan Analisis Lebih Lanjut
Suatu perusahaan investasi menawarkan rencana investasi dengan bunga majemuk. Investasi awal sebesar Rp 10.000.000,00 akan menghasilkan bunga 5% per tahun yang dikompositkan setiap tahun. Tentukan nilai investasi setelah 10 tahun dan berapa lama investasi tersebut akan mencapai Rp 20.000.000,00. Penyelesaian soal ini melibatkan pemahaman tentang pertumbuhan eksponensial dan penggunaan rumus barisan geometri untuk menghitung nilai investasi pada waktu tertentu.
Untuk menentukan waktu yang dibutuhkan hingga mencapai Rp 20.000.000,00, diperlukan penyelesaian persamaan eksponensial.
Ulasan Penutup: Contoh Soal Barisan Geometri
Setelah mempelajari berbagai contoh soal barisan geometri dan teknik penyelesaiannya, diharapkan pemahaman Anda tentang konsep ini semakin matang. Mulai dari soal-soal sederhana hingga yang lebih kompleks, kemampuan untuk mengidentifikasi pola dan menerapkan rumus yang tepat akan sangat membantu. Ingatlah bahwa latihan yang konsisten adalah kunci untuk menguasai materi ini. Dengan pemahaman yang kuat tentang barisan geometri, Anda akan siap menghadapi tantangan matematika lainnya dengan lebih percaya diri.