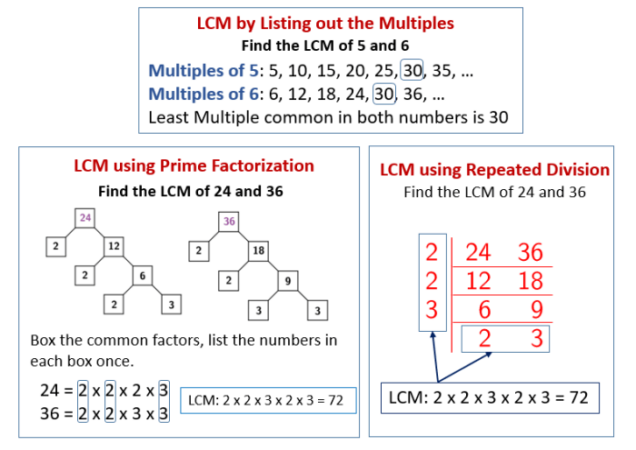
Contoh Soal KPK dan FPB, merupakan topik matematika yang penting untuk dipahami. Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB) seringkali muncul dalam kehidupan sehari-hari, mulai dari membagi kue hingga merencanakan kegiatan bersama. Memahami konsep ini akan membantu menyelesaikan berbagai permasalahan yang melibatkan pembagian dan pengelompokan.
Artikel ini akan membahas pengertian KPK dan FPB, metode pencariannya, contoh soal beserta penyelesaiannya, penerapan dalam kehidupan nyata, dan soal latihan untuk menguji pemahaman Anda. Dengan penjelasan yang sistematis dan contoh soal yang beragam, diharapkan pemahaman Anda tentang KPK dan FPB akan semakin terasah.
Pengertian KPK dan FPB
Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB) merupakan dua konsep penting dalam matematika yang berkaitan dengan bilangan bulat. Memahami keduanya sangat krusial dalam menyelesaikan berbagai permasalahan matematika, terutama yang melibatkan pecahan dan operasi bilangan. Kedua konsep ini saling berkaitan, namun memiliki perbedaan yang signifikan dalam cara perhitungan dan aplikasinya.
Definisi KPK dan FPB
Kelipatan Persekutuan Terkecil (KPK) dari dua bilangan atau lebih adalah bilangan terkecil yang merupakan kelipatan dari semua bilangan tersebut. Sedangkan Faktor Persekutuan Terbesar (FPB) dari dua bilangan atau lebih adalah bilangan terbesar yang merupakan faktor dari semua bilangan tersebut.
Contoh KPK dan FPB
Mari kita ambil contoh bilangan 6 dan 8. Kelipatan dari 6 adalah 6, 12, 18, 24, 30, … dan kelipatan dari 8 adalah 8, 16, 24, 32, … Kelipatan persekutuan dari 6 dan 8 adalah 24, 48, 72, dan seterusnya. Bilangan terkecil di antara kelipatan persekutuan tersebut adalah 24, sehingga KPK dari 6 dan 8 adalah 24.
Faktor dari 6 adalah 1, 2, 3, dan 6. Faktor dari 8 adalah 1, 2, 4, dan 8. Faktor persekutuan dari 6 dan 8 adalah 1 dan 2. Faktor persekutuan terbesar di antara keduanya adalah 2, sehingga FPB dari 6 dan 8 adalah 2.
Perbandingan KPK dan FPB
KPK dan FPB merupakan konsep yang saling berlawanan namun saling melengkapi. KPK mencari bilangan terkecil yang merupakan kelipatan bersama, sementara FPB mencari bilangan terbesar yang merupakan faktor bersama. KPK digunakan ketika kita perlu mencari nilai terkecil yang memenuhi beberapa kondisi kelipatan, misalnya dalam menentukan waktu pertemuan kembali dua kejadian periodik. FPB digunakan ketika kita perlu mencari nilai terbesar yang dapat membagi habis beberapa bilangan, misalnya dalam menyederhanakan pecahan.
Metode Penentuan KPK dan FPB
| Metode | KPK | FPB |
|---|---|---|
| Metode Faktorisasi Prima | Tentukan faktor prima dari masing-masing bilangan, lalu kalikan faktor prima yang paling banyak muncul untuk setiap faktor. | Tentukan faktor prima dari masing-masing bilangan, lalu kalikan faktor prima yang sama dengan pangkat terkecil. |
| Metode Kelipatan | Daftar kelipatan dari masing-masing bilangan hingga ditemukan kelipatan persekutuan terkecil. | Daftar faktor dari masing-masing bilangan hingga ditemukan faktor persekutuan terbesar. |
| Metode KPK dan FPB (Rumus) | KPK (a, b) = (a x b) / FPB (a, b) | – |
Ilustrasi Perbedaan KPK dan FPB
Bayangkan dua roda gigi dengan jumlah gigi berbeda. KPK menggambarkan jumlah putaran minimum yang dibutuhkan agar kedua roda gigi kembali ke posisi awal yang sama. FPB menggambarkan jumlah gigi terbesar yang dapat membagi habis jumlah gigi kedua roda gigi tersebut.
Metode Mencari KPK dan FPB
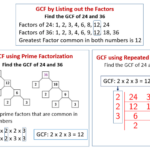
Mencari Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB) merupakan keterampilan dasar dalam matematika. Pemahaman yang baik tentang kedua konsep ini sangat penting untuk menyelesaikan berbagai permasalahan, terutama dalam aritmatika dan aljabar. Berikut ini akan diuraikan beberapa metode untuk mencari KPK dan FPB, beserta perbandingan efisiensi antar metode.
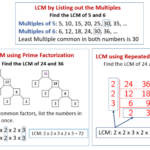
Mencari KPK dengan Metode Faktorisasi Prima
Metode faktorisasi prima merupakan cara efektif untuk menentukan KPK. Langkah-langkahnya sebagai berikut: Faktorkan setiap bilangan menjadi faktor prima. Kemudian, kalikan faktor prima yang paling banyak muncul pada setiap faktorisasi. Hasil perkalian tersebut adalah KPK.
Contoh: Cari KPK dari 12 dan 18.
- Faktorisasi prima 12: 2 x 2 x 3 = 2 2 x 3
- Faktorisasi prima 18: 2 x 3 x 3 = 2 x 3 2
- KPK(12, 18) = 2 2 x 3 2 = 4 x 9 = 36
Mencari FPB dengan Metode Faktorisasi Prima
Menentukan FPB dengan metode faktorisasi prima juga relatif mudah. Langkah-langkahnya adalah sebagai berikut: Faktorkan setiap bilangan menjadi faktor prima. Kemudian, pilih faktor prima yang sama dan memiliki pangkat terkecil. Hasil perkalian faktor-faktor tersebut adalah FPB.
Contoh: Cari FPB dari 12 dan 18.
- Faktorisasi prima 12: 2 x 2 x 3 = 2 2 x 3
- Faktorisasi prima 18: 2 x 3 x 3 = 2 x 3 2
- FPB(12, 18) = 2 x 3 = 6
Mencari KPK dan FPB Menggunakan Tabel
Metode tabel menawarkan pendekatan sistematis untuk mencari KPK dan FPB. Buat tabel yang berisi bilangan yang akan dicari KPK dan FPB-nya, lalu faktorkan setiap bilangan tersebut secara berurutan. KPK diperoleh dari perkalian semua faktor prima yang muncul, dengan pangkat tertinggi. FPB diperoleh dari perkalian faktor prima yang sama dengan pangkat terendah.
Contoh: Cari KPK dan FPB dari 12, 18, dan 24.
| Bilangan | Faktorisasi Prima |
|---|---|
| 12 | 22 x 3 |
| 18 | 2 x 32 |
| 24 | 23 x 3 |
KPK(12, 18, 24) = 2 3 x 3 2 = 8 x 9 = 72
FPB(12, 18, 24) = 2 x 3 = 6
Mencari KPK dan FPB dari Tiga Bilangan Menggunakan Metode Pohon Faktor
Metode pohon faktor memberikan visualisasi yang jelas dalam proses faktorisasi prima. Buat pohon faktor untuk setiap bilangan. Kemudian, tentukan KPK dan FPB dengan cara yang sama seperti pada metode faktorisasi prima.
Contoh: Cari KPK dan FPB dari 12, 18, dan 24 menggunakan pohon faktor.
Ilustrasi pohon faktor untuk 12, 18, dan 24 akan menunjukkan cabang-cabang yang menuju ke faktor prima masing-masing. Dari sana, kita dapat dengan mudah mengidentifikasi faktor prima yang sama dan pangkat tertinggi (untuk KPK) dan faktor prima yang sama dengan pangkat terendah (untuk FPB). KPK(12, 18, 24) = 72 dan FPB(12, 18, 24) = 6.
Perbandingan Efisiensi Metode Faktorisasi Prima dan Metode Tabel
Baik metode faktorisasi prima maupun metode tabel efektif dalam mencari KPK dan FPB. Namun, metode tabel mungkin lebih mudah dipahami dan divisualisasikan, terutama untuk bilangan yang lebih besar atau jumlah bilangan yang lebih banyak. Metode faktorisasi prima mungkin lebih efisien untuk bilangan yang relatif kecil, karena membutuhkan langkah-langkah yang lebih sedikit.
Contoh Soal dan Penyelesaian KPK dan FPB: Contoh Soal Kpk Dan Fpb
Kemampuan menentukan Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB) sangat penting dalam menyelesaikan berbagai permasalahan matematika, khususnya yang berkaitan dengan pengukuran, pembagian, dan penjadwalan. Pemahaman yang baik tentang konsep KPK dan FPB akan memudahkan kita dalam menyelesaikan soal-soal cerita yang melibatkan kedua konsep tersebut.
Berikut ini beberapa contoh soal cerita yang akan kita bahas, beserta penyelesaiannya menggunakan metode faktorisasi prima dan metode tabel. Kita akan fokus pada pemahaman langkah-langkah penyelesaian, sehingga Anda dapat mengaplikasikannya pada soal-soal lain yang serupa.
Contoh Soal Cerita Mencari KPK
Berikut lima contoh soal cerita yang melibatkan pencarian KPK. Soal-soal ini menggambarkan situasi nyata di mana menentukan KPK sangatlah berguna.
- Dua buah lampu A dan B menyala secara bergantian. Lampu A menyala setiap 3 menit, sedangkan lampu B menyala setiap 5 menit. Kapan kedua lampu tersebut menyala bersamaan untuk pertama kalinya?
- Ani berenang setiap 4 hari sekali, Budi setiap 6 hari sekali, dan Cici setiap 8 hari sekali. Pada tanggal 1 Januari mereka berenang bersama-sama. Kapan mereka akan berenang bersama lagi?
- Pak Budi memanen padi setiap 12 hari sekali, sedangkan Pak Amir memanen jagung setiap 15 hari sekali. Jika hari ini mereka memanen bersamaan, kapan mereka akan memanen bersama lagi?
- Dua buah bus berangkat dari terminal yang sama. Bus A berangkat setiap 20 menit, dan bus B berangkat setiap 30 menit. Berapa menit lagi kedua bus akan berangkat bersamaan?
- Sebuah mesin A berputar setiap 10 detik, dan mesin B berputar setiap 15 detik. Kapan kedua mesin akan berputar bersamaan untuk kedua kalinya?
Contoh Soal Cerita Mencari FPB
Berikut lima contoh soal cerita yang melibatkan pencarian FPB. Soal-soal ini menunjukkan penerapan FPB dalam konteks praktis.
- Ibu memiliki 12 buah apel dan 18 buah jeruk. Ibu ingin membagi buah-buah tersebut ke dalam beberapa kantong dengan jumlah apel dan jeruk yang sama banyak di setiap kantong. Berapa banyak kantong yang dibutuhkan Ibu?
- Pak Amir memiliki 24 pensil dan 36 buku tulis. Ia ingin membagi pensil dan buku tulis tersebut kepada beberapa anak dengan jumlah pensil dan buku tulis yang sama banyak untuk setiap anak. Berapa banyak anak yang bisa menerima pembagian tersebut?
- Ada dua pita dengan panjang 30 cm dan 45 cm. Kedua pita tersebut akan dipotong menjadi beberapa potongan dengan panjang yang sama. Berapa panjang potongan terbesar yang bisa dibuat?
- Sebuah persegi panjang memiliki panjang 48 cm dan lebar 36 cm. Persegi panjang tersebut akan dibagi menjadi beberapa persegi kecil dengan ukuran yang sama. Berapa panjang sisi persegi kecil terbesar yang mungkin?
- Andi memiliki 60 kelereng merah dan 75 kelereng biru. Ia ingin memasukkan kelereng tersebut ke dalam beberapa toples dengan jumlah kelereng merah dan biru yang sama banyak di setiap toples. Berapa banyak toples yang dibutuhkan Andi?
Penyelesaian Contoh Soal KPK Menggunakan Metode Faktorisasi Prima
Metode faktorisasi prima merupakan cara efektif untuk menentukan KPK dan FPB. Berikut penyelesaian soal nomor 1 dan 2 menggunakan metode ini.
- Soal 1: Lampu A (3 menit), Lampu B (5 menit). Faktorisasi prima: 3 = 3; 5 = 5. KPK (3, 5) = 3 x 5 = 15 menit. Kedua lampu akan menyala bersamaan untuk pertama kalinya setelah 15 menit.
- Soal 2: Ani (4 hari), Budi (6 hari), Cici (8 hari). Faktorisasi prima: 4 = 2 x 2; 6 = 2 x 3; 8 = 2 x 2 x 2. KPK (4, 6, 8) = 2 x 2 x 2 x 3 = 24 hari. Mereka akan berenang bersama lagi setelah 24 hari.
Penyelesaian Contoh Soal KPK Menggunakan Metode Tabel
Metode tabel juga merupakan alternatif yang mudah dipahami untuk menentukan KPK. Berikut penyelesaian soal nomor 3 dan 4 menggunakan metode ini.
- Soal 3: Pak Budi (12 hari), Pak Amir (15 hari).
Kelipatan 12 12 24 36 48 60 Kelipatan 15 15 30 45 60 KPK (12, 15) = 60 hari. Mereka akan memanen bersama lagi setelah 60 hari.
- Soal 4: Bus A (20 menit), Bus B (30 menit).
Kelipatan 20 20 40 60 Kelipatan 30 30 60 KPK (20, 30) = 60 menit. Kedua bus akan berangkat bersamaan lagi setelah 60 menit.
Penyelesaian Contoh Soal FPB Menggunakan Metode Faktorisasi Prima
Berikut rangkuman langkah-langkah penyelesaian soal nomor 5 mencari FPB menggunakan metode faktorisasi prima.
Langkah 1: Tentukan faktor prima dari masing-masing angka.
Langkah 2: Identifikasi faktor prima yang sama pada kedua angka tersebut.
Langkah 3: Kalikan faktor prima yang sama tersebut. Hasilnya adalah FPB.
Penerapan KPK dan FPB dalam Kehidupan Sehari-hari
Kemampuan menentukan Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB) bukan hanya sebatas materi pelajaran matematika. Keduanya memiliki aplikasi praktis dalam berbagai situasi kehidupan sehari-hari, membantu kita menyelesaikan masalah dengan lebih efisien dan efektif. Memahami konsep ini akan memudahkan kita dalam berbagai aktivitas, mulai dari membagi barang hingga mengatur jadwal.
Contoh Penerapan KPK dalam Kehidupan Sehari-hari
KPK berguna ketika kita perlu mencari kelipatan terkecil dari beberapa angka. Dalam konteks kehidupan sehari-hari, hal ini sangat membantu dalam menyelaraskan jadwal atau aktivitas yang berulang.
- Menentukan jadwal pertemuan: Misalnya, tiga teman ingin bertemu setiap minggu. Teman pertama datang setiap 3 hari, teman kedua setiap 4 hari, dan teman ketiga setiap 6 hari. Untuk menentukan kapan mereka dapat bertemu bersama, kita perlu mencari KPK dari 3, 4, dan 6, yaitu 12. Jadi, mereka dapat bertemu setiap 12 hari.
- Menentukan waktu keberangkatan bus: Dua jalur bus berbeda melewati sebuah halte. Bus jalur A datang setiap 15 menit, sementara bus jalur B datang setiap 20 menit. Untuk mengetahui kapan kedua bus akan tiba di halte secara bersamaan, kita perlu mencari KPK dari 15 dan 20, yaitu 60. Artinya, kedua bus akan tiba di halte bersamaan setiap 60 menit atau 1 jam.
- Membeli barang dalam kemasan: Bayangkan Anda ingin membeli permen yang dikemas dalam kotak berisi 6 buah dan cokelat yang dikemas dalam kotak berisi 8 buah. Untuk mendapatkan jumlah permen dan cokelat yang sama banyak, Anda perlu mencari KPK dari 6 dan 8, yaitu 24. Artinya, Anda harus membeli 4 kotak permen (4 x 6 = 24) dan 3 kotak cokelat (3 x 8 = 24).
Contoh Penerapan FPB dalam Kehidupan Sehari-hari
FPB berguna ketika kita perlu mencari faktor terbesar yang sama dari beberapa angka. Konsep ini sering diterapkan dalam kegiatan yang melibatkan pengelompokan atau pembagian.
- Membagi kue: Anda memiliki 12 kue cokelat dan 18 kue vanila. Anda ingin membagi kue tersebut ke dalam beberapa kotak dengan jumlah kue cokelat dan vanila yang sama banyak di setiap kotak. Untuk menentukan jumlah maksimum kotak yang bisa dibuat, kita perlu mencari FPB dari 12 dan 18, yaitu 6. Jadi, Anda dapat membuat 6 kotak, masing-masing berisi 2 kue cokelat dan 3 kue vanila.
- Mengatur tanaman dalam pot: Anda memiliki 24 tanaman mawar dan 36 tanaman anggrek. Anda ingin menanamnya dalam beberapa pot dengan jumlah mawar dan anggrek yang sama banyak di setiap pot. Untuk menentukan jumlah maksimum pot yang dapat digunakan, kita perlu mencari FPB dari 24 dan 36, yaitu 12. Jadi, Anda dapat membuat 12 pot, masing-masing berisi 2 tanaman mawar dan 3 tanaman anggrek.
- Membuat kelompok siswa: Sebuah kelas terdiri dari 20 siswa laki-laki dan 28 siswa perempuan. Guru ingin membagi siswa ke dalam beberapa kelompok dengan jumlah siswa laki-laki dan perempuan yang sama banyak di setiap kelompok. Untuk menentukan jumlah maksimum kelompok yang dapat dibentuk, kita perlu mencari FPB dari 20 dan 28, yaitu 4. Jadi, guru dapat membentuk 4 kelompok, masing-masing berisi 5 siswa laki-laki dan 7 siswa perempuan.
Penggunaan KPK dalam Menyelesaikan Masalah Pembagian Barang
KPK sangat membantu dalam memastikan pembagian barang secara adil dan merata, terutama jika barang tersebut memiliki jumlah yang berbeda dan kita ingin membaginya ke dalam beberapa bagian yang sama. Dengan mencari KPK, kita dapat menentukan jumlah minimum barang yang dibutuhkan agar setiap bagian memiliki jumlah yang sama tanpa ada sisa.
Penggunaan FPB dalam Menyelesaikan Masalah Pengelompokan
FPB membantu kita dalam menentukan ukuran kelompok terbesar yang mungkin saat mengelompokkan sejumlah barang atau individu. Ini memastikan bahwa setiap kelompok memiliki jumlah anggota yang sama dan optimal, memaksimalkan efisiensi dan keseragaman dalam pengelompokan.
Skenario Permasalahan yang Melibatkan KPK dan FPB Secara Bersamaan
Sebuah sekolah akan mengadakan acara perpisahan. Panitia ingin menyediakan kue dan minuman untuk 36 siswa kelas 6 dan 48 siswa kelas 9. Mereka ingin membagi kue dan minuman ke dalam beberapa kelompok dengan jumlah siswa kelas 6 dan 9 yang sama banyak di setiap kelompok. Berapa jumlah maksimum kelompok yang dapat dibentuk? Berapa banyak kue dan minuman yang harus disediakan agar setiap kelompok mendapatkan jumlah yang sama?
Untuk menyelesaikan masalah ini, kita perlu mencari FPB dari 36 dan 48 untuk menentukan jumlah maksimum kelompok (FPB dari 36 dan 48 adalah 12). Kemudian, kita perlu mencari KPK dari jumlah kue dan minuman yang ingin disediakan per kelompok agar jumlahnya sama rata untuk semua kelompok.
Soal Latihan KPK dan FPB

Setelah mempelajari konsep Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB), mari kita uji pemahaman Anda melalui beberapa soal latihan. Soal-soal berikut disusun dalam bentuk pilihan ganda dan uraian untuk mengasah kemampuan Anda dalam menyelesaikan masalah yang berkaitan dengan KPK dan FPB.
Penguasaan KPK dan FPB sangat penting dalam berbagai bidang, mulai dari memecahkan masalah matematika sehari-hari hingga aplikasi dalam ilmu teknik dan komputer. Kemampuan untuk menemukan KPK dan FPB dengan cepat dan akurat akan sangat membantu dalam menyelesaikan berbagai permasalahan.
Soal Latihan KPK Pilihan Ganda
Berikut lima soal pilihan ganda untuk melatih perhitungan KPK dari dua bilangan. Pilihlah satu jawaban yang paling tepat.
- KPK dari 12 dan 18 adalah…
- A. 6
- B. 36
- C. 72
- D. 216
- A. 10
- B. 60
- C. 100
- D. 600
- A. 5
- B. 75
- C. 150
- D. 375
- A. 4
- B. 24
- C. 48
- D. 96
- A. 3
- B. 45
- C. 135
- D. 225
Soal Latihan FPB Pilihan Ganda
Berikut lima soal pilihan ganda untuk melatih perhitungan FPB dari tiga bilangan. Pilihlah satu jawaban yang paling tepat.
- FPB dari 12, 18, dan 24 adalah…
- A. 2
- B. 3
- C. 6
- D. 12
- A. 1
- B. 5
- C. 15
- D. 75
- A. 6
- B. 12
- C. 24
- D. 144
- A. 4
- B. 8
- C. 16
- D. 48
- A. 3
- B. 6
- C. 9
- D. 18
Soal Latihan KPK Uraian
Berikut lima soal uraian untuk melatih perhitungan KPK dari dua bilangan. Tunjukkan langkah-langkah penyelesaian Anda.
- Tentukan KPK dari 24 dan 36.
- Tentukan KPK dari 15 dan 45.
- Tentukan KPK dari 18 dan 27.
- Tentukan KPK dari 20 dan 40.
- Tentukan KPK dari 16 dan 24.
Soal Latihan FPB Uraian, Contoh soal kpk dan fpb
Berikut lima soal uraian untuk melatih perhitungan FPB dari tiga bilangan. Tunjukkan langkah-langkah penyelesaian Anda.
- Tentukan FPB dari 24, 36, dan 48.
- Tentukan FPB dari 15, 20, dan 25.
- Tentukan FPB dari 18, 27, dan 36.
- Tentukan FPB dari 12, 18, dan 30.
- Tentukan FPB dari 20, 30, dan 40.
Kunci Jawaban
Berikut kunci jawaban untuk soal-soal latihan di atas:
Pilihan Ganda KPK: 1. B, 2. B, 3. B, 4. B, 5.
B
Pilihan Ganda FPB: 1. C, 2. B, 3. B, 4. B, 5.
C
Uraian KPK: Penyelesaian uraian memerlukan langkah-langkah faktorisasi prima atau kelipatan masing-masing bilangan untuk menentukan KPK.
Uraian FPB: Penyelesaian uraian memerlukan langkah-langkah faktorisasi prima masing-masing bilangan untuk menentukan FPB.
Terakhir
Setelah mempelajari contoh soal KPK dan FPB, diharapkan Anda dapat dengan mudah mengaplikasikan konsep ini dalam berbagai situasi. Menguasai KPK dan FPB tidak hanya penting untuk menyelesaikan soal matematika, tetapi juga berguna dalam memecahkan masalah praktis dalam kehidupan sehari-hari. Latihan terus-menerus akan meningkatkan kemampuan Anda dalam menentukan KPK dan FPB dengan cepat dan tepat.