- Prisma Segitiga
- Rumus Luas Permukaan Prisma Segitiga
-
Contoh Soal dan Pembahasan Luas Permukaan Prisma Segitiga: Contoh Soal Luas Permukaan Prisma Segitiga
- Soal dan Pembahasan Luas Permukaan Prisma Segitiga
- Soal 1: Prisma Segitiga Sederhana
- Soal 2: Prisma Segitiga dengan Alas Segitiga Sama Kaki
- Soal 3: Prisma Segitiga dengan Alas Segitiga Sembarang
- Soal 4: Prisma Segitiga Beraturan dengan Tinggi yang Berbeda
- Soal 5: Prisma Segitiga dengan Modifikasi
- Tabel Ringkasan
- Perbedaan Pendekatan Penyelesaian
- Penerapan Luas Permukaan Prisma Segitiga dalam Kehidupan Nyata
- Ringkasan Akhir
Contoh soal luas permukaan prisma segitiga merupakan kunci untuk memahami konsep geometri ruang tiga dimensi. Memahami rumus dan penerapannya dalam berbagai soal cerita akan membantu kita menyelesaikan permasalahan yang berkaitan dengan bangun ruang ini, baik dalam konteks akademis maupun kehidupan sehari-hari. Prisma segitiga, dengan bentuknya yang unik, sering ditemukan dalam berbagai objek di sekitar kita, mulai dari atap rumah hingga kemasan makanan.
Artikel ini akan membahas secara detail tentang prisma segitiga, mulai dari definisi, unsur-unsur penyusun, rumus luas permukaan, hingga contoh soal dan pembahasannya. Dengan pemahaman yang komprehensif, diharapkan pembaca dapat dengan mudah menghitung luas permukaan prisma segitiga dan mengaplikasikannya dalam berbagai situasi.
Prisma Segitiga
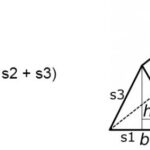
Prisma segitiga merupakan bangun ruang tiga dimensi yang dibatasi oleh dua buah bidang segitiga yang sejajar dan kongruen (sebangun dan sama besar) sebagai alas dan atap, serta tiga buah bidang persegi panjang sebagai sisi tegak. Bentuknya yang unik dan relatif sederhana membuatnya sering dijumpai dalam berbagai objek di sekitar kita.
Unsur-unsur Prisma Segitiga
Prisma segitiga tersusun atas beberapa unsur penting yang membentuk bangun ruang tersebut. Memahami unsur-unsur ini krusial untuk menghitung luas permukaan dan volume prisma segitiga.
- Sisi: Prisma segitiga memiliki 5 sisi; 2 sisi berbentuk segitiga (alas dan atap) dan 3 sisi berbentuk persegi panjang (sisi tegak).
- Rusuk: Terdapat 9 rusuk pada prisma segitiga; 3 rusuk pada masing-masing alas dan atap, dan 3 rusuk yang menghubungkan alas dan atap.
- Titik Sudut: Prisma segitiga memiliki 6 titik sudut; 3 titik sudut pada alas dan 3 titik sudut pada atap.
Ilustrasi Prisma Segitiga, Contoh soal luas permukaan prisma segitiga
Bayangkan sebuah prisma segitiga dengan alas berupa segitiga sama sisi dengan panjang sisi 5 cm dan tinggi segitiga 4,33 cm. Ketiga sisi tegaknya berupa persegi panjang dengan panjang 10 cm (tinggi prisma) dan lebar 5 cm (panjang sisi alas segitiga). Atap prisma merupakan segitiga sama sisi yang kongruen dengan alasnya. Setiap rusuk yang menghubungkan alas dan atap tegak lurus terhadap alas dan atap.
Sudut-sudut yang dibentuk oleh pertemuan rusuk-rusuk membentuk sudut siku-siku pada sisi tegak dan sudut 60 derajat pada alas dan atap (karena alas dan atap berbentuk segitiga sama sisi).
Perbandingan Prisma Segitiga dengan Bangun Ruang Lainnya
Untuk memahami karakteristik prisma segitiga lebih baik, mari kita bandingkan dengan beberapa bangun ruang lainnya. Perbedaan pada bentuk alas, jumlah sisi, dan jumlah rusuk menjadi pembeda utama.
| Karakteristik | Prisma Segitiga | Kubus | Balok | Limas Segitiga |
|---|---|---|---|---|
| Bentuk Alas | Segitiga | Bujur sangkar | Persegi panjang | Segitiga |
| Jumlah Sisi | 5 | 6 | 6 | 4 |
| Jumlah Rusuk | 9 | 12 | 12 | 6 |
| Jumlah Titik Sudut | 6 | 8 | 8 | 4 |
Rumus Luas Permukaan Prisma Segitiga
Prisma segitiga merupakan bangun ruang tiga dimensi yang memiliki dua sisi berbentuk segitiga kongruen (sama dan sebangun) sebagai alas dan atas, serta tiga sisi tegak berbentuk persegi panjang yang menghubungkan alas dan atas. Menghitung luas permukaan prisma segitiga penting dalam berbagai aplikasi, mulai dari perencanaan konstruksi hingga desain kemasan.
Memahami rumus dan langkah-langkah perhitungannya akan membantu kita menyelesaikan berbagai permasalahan yang berkaitan dengan luas permukaan bangun ruang ini.
Rumus Luas Permukaan Prisma Segitiga
Luas permukaan prisma segitiga merupakan jumlah luas seluruh sisi penyusunnya. Rumus umum yang digunakan adalah:
Lp = 2 x Luas Alas + Keliling Alas x Tinggi Prisma
di mana:
- Lp = Luas Permukaan Prisma Segitiga
- Luas Alas = Luas segitiga yang membentuk alas prisma (½ x alas segitiga x tinggi segitiga)
- Keliling Alas = Jumlah panjang ketiga sisi segitiga yang membentuk alas prisma
- Tinggi Prisma = Jarak antara kedua bidang alas segitiga.
Langkah-langkah perhitungannya meliputi menghitung luas alas segitiga, keliling alas segitiga, dan kemudian mensubstitusikan nilai-nilai tersebut ke dalam rumus luas permukaan.
Contoh Perhitungan Luas Permukaan Prisma Segitiga
Berikut beberapa contoh perhitungan dengan ukuran yang berbeda-beda untuk memperjelas pemahaman:
Contoh 1: Prisma segitiga dengan alas segitiga siku-siku berukuran 3 cm, 4 cm, dan 5 cm (hipotenusa), serta tinggi prisma 10 cm.
Luas Alas = ½ x 3 cm x 4 cm = 6 cm²
Keliling Alas = 3 cm + 4 cm + 5 cm = 12 cm
Lp = 2 x 6 cm² + 12 cm x 10 cm = 12 cm² + 120 cm² = 132 cm²
Contoh 2: Prisma segitiga dengan alas segitiga sama sisi berukuran 6 cm dan tinggi prisma 8 cm.
Luas Alas = ½ x 6 cm x (6 cm x √3/2) ≈ 15.59 cm²
Keliling Alas = 3 x 6 cm = 18 cm
Lp = 2 x 15.59 cm² + 18 cm x 8 cm ≈ 31.18 cm² + 144 cm² ≈ 175.18 cm²
Contoh 3: Prisma segitiga dengan alas segitiga sembarang berukuran 5 cm, 7 cm, dan 8 cm, serta tinggi prisma 12 cm. Misalkan tinggi segitiga pada alas adalah 4 cm.
Luas Alas = ½ x 5 cm x 4 cm = 10 cm²
Keliling Alas = 5 cm + 7 cm + 8 cm = 20 cm
Lp = 2 x 10 cm² + 20 cm x 12 cm = 20 cm² + 240 cm² = 260 cm²
Contoh Soal Cerita dan Penyelesaiannya
Sebuah tenda berbentuk prisma segitiga memiliki alas berbentuk segitiga sama kaki dengan panjang sisi alas 2 meter dan sisi miring 2.5 meter. Tinggi tenda 3 meter. Berapa luas kain yang dibutuhkan untuk membuat tenda tersebut (abaikan bagian bawah tenda)?
Penyelesaian:
- Menghitung tinggi segitiga alas: Kita dapat menggunakan teorema Pythagoras pada segitiga siku-siku yang terbentuk dengan membagi segitiga sama kaki menjadi dua segitiga siku-siku. Tinggi segitiga alas adalah √(2.5² – 1²) ≈ 2.29 meter.
- Menghitung luas alas: Luas alas = ½ x 2 m x 2.29 m ≈ 2.29 m²
- Menghitung keliling alas: Keliling alas = 2 m + 2.5 m + 2.5 m = 7 m
- Menghitung luas permukaan tenda (tanpa alas bawah): Luas permukaan = 2 x Luas Alas + Keliling Alas x Tinggi Tenda = 2 x 2.29 m² + 7 m x 3 m = 4.58 m² + 21 m² = 25.58 m²
- Jadi, luas kain yang dibutuhkan untuk membuat tenda tersebut sekitar 25.58 meter persegi.
Contoh Soal dan Pembahasan Luas Permukaan Prisma Segitiga: Contoh Soal Luas Permukaan Prisma Segitiga
Menghitung luas permukaan prisma segitiga merupakan aplikasi penting dari konsep geometri ruang. Memahami perhitungan ini bermanfaat dalam berbagai bidang, mulai dari arsitektur hingga teknik sipil, bahkan dalam pembuatan kemasan produk. Berikut beberapa contoh soal dengan tingkat kesulitan bervariasi, disertai pembahasan lengkapnya.
Soal dan Pembahasan Luas Permukaan Prisma Segitiga
Berikut lima soal cerita yang menggambarkan perhitungan luas permukaan prisma segitiga dengan tingkat kesulitan yang berbeda, disertai ilustrasi dan pembahasannya.
Soal 1: Prisma Segitiga Sederhana
Sebuah prisma segitiga memiliki alas berbentuk segitiga siku-siku dengan panjang sisi siku-sikunya 6 cm dan 8 cm. Tinggi prisma tersebut adalah 10 cm. Tentukan luas permukaan prisma segitiga tersebut.
Ilustrasi: Prisma segitiga dengan alas segitiga siku-siku (6 cm, 8 cm) dan tinggi prisma 10 cm. Sisi miring alas segitiga dapat dihitung menggunakan teorema Pythagoras (√(6² + 8²) = 10 cm). Ketiga sisi tegak prisma berbentuk persegi panjang dengan ukuran 10 cm x 6 cm, 10 cm x 8 cm, dan 10 cm x 10 cm.
Pembahasan: Luas alas segitiga = (1/2) x 6 cm x 8 cm = 24 cm². Luas permukaan sisi tegak = (6 cm x 10 cm) + (8 cm x 10 cm) + (10 cm x 10 cm) = 240 cm². Luas permukaan total = (2 x luas alas) + luas permukaan sisi tegak = (2 x 24 cm²) + 240 cm² = 288 cm².
Soal 2: Prisma Segitiga dengan Alas Segitiga Sama Kaki
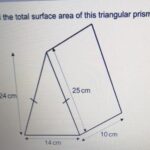
Sebuah tenda berbentuk prisma segitiga dengan alas segitiga sama kaki. Panjang sisi alasnya 12 cm, tinggi alasnya 8 cm, dan tinggi tenda (tinggi prisma) 20 cm. Hitung luas permukaan tenda tersebut.
Ilustrasi: Prisma segitiga dengan alas segitiga sama kaki (sisi alas 12 cm, tinggi alas 8 cm) dan tinggi prisma 20 cm. Sisi tegak prisma berbentuk persegi panjang dengan ukuran 20 cm x 12 cm (dua buah) dan 20 cm x sisi miring segitiga alas.
Pembahasan: Luas alas segitiga = (1/2) x 12 cm x 8 cm = 48 cm². Sisi miring segitiga alas = √((12/2)² + 8²) = 10 cm. Luas permukaan sisi tegak = (2 x 12 cm x 20 cm) + (10 cm x 20 cm) = 600 cm². Luas permukaan total = (2 x 48 cm²) + 600 cm² = 696 cm².
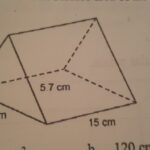
Soal 3: Prisma Segitiga dengan Alas Segitiga Sembarang
Sebuah prisma segitiga memiliki alas berupa segitiga dengan panjang sisi 5 cm, 7 cm, dan 8 cm. Tinggi prisma adalah 12 cm. Tentukan luas permukaan prisma tersebut. Gunakan rumus Heron untuk menghitung luas alas.
Ilustrasi: Prisma segitiga dengan alas segitiga sembarang (sisi 5 cm, 7 cm, 8 cm) dan tinggi prisma 12 cm. Ketiga sisi tegak prisma berbentuk persegi panjang dengan ukuran 12 cm x 5 cm, 12 cm x 7 cm, dan 12 cm x 8 cm.
Pembahasan: Menghitung luas alas menggunakan rumus Heron. s = (5+7+8)/2 = 10. Luas alas = √(10(10-5)(10-7)(10-8)) = √(10 x 5 x 3 x 2) = √300 ≈ 17.32 cm². Luas permukaan sisi tegak = (5 cm x 12 cm) + (7 cm x 12 cm) + (8 cm x 12 cm) = 240 cm². Luas permukaan total ≈ (2 x 17.32 cm²) + 240 cm² ≈ 274.64 cm².
Soal 4: Prisma Segitiga Beraturan dengan Tinggi yang Berbeda
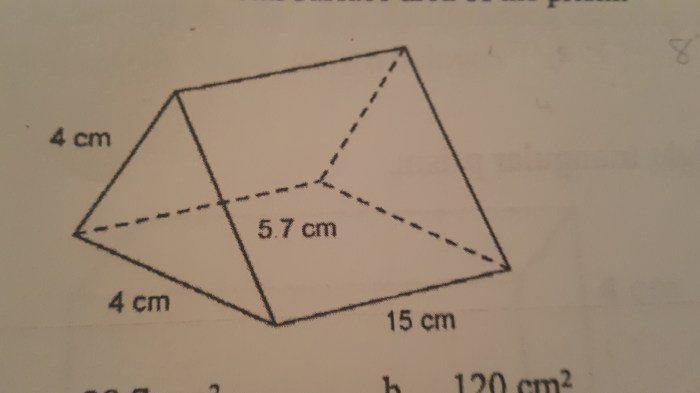
Sebuah prisma segitiga beraturan memiliki panjang sisi alas 4 cm dan tinggi prisma 15 cm. Tentukan luas permukaan prisma tersebut.
Ilustrasi: Prisma segitiga beraturan (segitiga sama sisi dengan sisi 4 cm) dengan tinggi prisma 15 cm. Ketiga sisi tegak prisma berbentuk persegi panjang dengan ukuran 15 cm x 4 cm.
Pembahasan: Luas alas segitiga sama sisi = (√3/4) x 4² cm² = 4√3 cm². Luas permukaan sisi tegak = 3 x (4 cm x 15 cm) = 180 cm². Luas permukaan total = (2 x 4√3 cm²) + 180 cm² ≈ 193.9 cm².
Soal 5: Prisma Segitiga dengan Modifikasi
Sebuah prisma segitiga memiliki alas berbentuk segitiga siku-siku dengan sisi-sisi 3 cm, 4 cm, dan 5 cm. Tinggi prisma 8 cm. Jika bagian atas prisma dipotong sehingga membentuk prisma segitiga yang lebih kecil dengan tinggi 3 cm, tentukan luas permukaan prisma yang tersisa.
Ilustrasi: Prisma segitiga awal dengan alas segitiga siku-siku (3 cm, 4 cm, 5 cm) dan tinggi 8 cm. Bagian atas dipotong sehingga tersisa prisma dengan tinggi 5 cm.
Pembahasan: Luas alas = (1/2) x 3 cm x 4 cm = 6 cm². Luas permukaan sisi tegak prisma awal = (3 cm x 8 cm) + (4 cm x 8 cm) + (5 cm x 8 cm) = 96 cm². Luas permukaan prisma yang dipotong = (3 cm x 3 cm) + (4 cm x 3 cm) + (5 cm x 3 cm) + (2 x 6 cm²) = 42 cm².
Luas permukaan prisma yang tersisa = 96 cm² + 6 cm² + 6 cm²
-42 cm² = 66 cm².
Tabel Ringkasan
| Soal | Langkah Penyelesaian | Rumus yang Digunakan | Hasil |
|---|---|---|---|
| Soal 1 | Hitung luas alas dan luas sisi tegak, lalu jumlahkan | Luas permukaan = 2 x Luas alas + Luas sisi tegak | 288 cm² |
| Soal 2 | Hitung luas alas dan luas sisi tegak, lalu jumlahkan | Luas permukaan = 2 x Luas alas + Luas sisi tegak | 696 cm² |
| Soal 3 | Hitung luas alas (rumus Heron), lalu hitung luas sisi tegak dan jumlahkan | Luas permukaan = 2 x Luas alas + Luas sisi tegak | ≈ 274.64 cm² |
| Soal 4 | Hitung luas alas segitiga sama sisi, lalu hitung luas sisi tegak dan jumlahkan | Luas permukaan = 2 x Luas alas + Luas sisi tegak | ≈ 193.9 cm² |
| Soal 5 | Hitung luas permukaan prisma awal dan prisma yang dipotong, lalu kurangkan | Luas permukaan = Luas permukaan prisma awal – Luas permukaan prisma yang dipotong | 66 cm² |
Perbedaan Pendekatan Penyelesaian
Perbedaan pendekatan penyelesaian pada soal-soal di atas terutama terletak pada bentuk alas prisma segitiga. Soal yang lebih sederhana (Soal 1 dan 2) menggunakan alas segitiga siku-siku dan segitiga sama kaki yang mudah dihitung luasnya. Soal 3 menggunakan segitiga sembarang yang memerlukan rumus Heron. Soal 4 melibatkan segitiga sama sisi, sementara Soal 5 memerlukan perhitungan bertahap karena adanya modifikasi bentuk prisma.
Penerapan Luas Permukaan Prisma Segitiga dalam Kehidupan Nyata
Perhitungan luas permukaan prisma segitiga, meskipun terlihat rumit, memiliki aplikasi praktis yang signifikan dalam berbagai aspek kehidupan sehari-hari. Memahami konsep ini memungkinkan kita untuk menyelesaikan masalah praktis dan membuat keputusan yang lebih tepat dalam berbagai situasi.
Contoh Penerapan Luas Permukaan Prisma Segitiga dalam Kehidupan Sehari-hari
Berikut beberapa contoh penerapan perhitungan luas permukaan prisma segitiga dalam kehidupan nyata, disertai penjelasan rinci dan manfaatnya.
- Desain dan Pembuatan Rumah Kaca: Banyak rumah kaca modern menggunakan struktur prisma segitiga untuk atapnya. Perhitungan luas permukaan sangat penting untuk menentukan jumlah material yang dibutuhkan (kaca, rangka besi) dalam pembuatan rumah kaca tersebut. Dengan perhitungan yang akurat, kita dapat meminimalkan biaya material dan memastikan struktur yang kokoh. Memahami luas permukaan membantu memastikan efisiensi penggunaan material dan mengurangi limbah.
- Perencanaan Pembangunan Terowongan: Terowongan dengan penampang segitiga (atau yang dapat didekomposisi menjadi bentuk-bentuk segitiga) membutuhkan perhitungan luas permukaan untuk menentukan jumlah material yang dibutuhkan untuk melapisi dinding terowongan, baik dengan beton maupun material lainnya. Akurasi perhitungan ini sangat krusial untuk memastikan kekuatan struktur dan juga untuk memperkirakan biaya proyek. Ketepatan perhitungan luas permukaan memastikan efisiensi biaya dan konstruksi yang aman.
- Desain dan Pembuatan Kemasan Produk: Beberapa kemasan produk, terutama yang berbentuk unik, menggunakan prisma segitiga sebagai dasar desainnya. Perhitungan luas permukaan penting untuk menentukan jumlah material kemasan yang dibutuhkan dan juga untuk menentukan biaya produksi. Perhitungan yang akurat memastikan efisiensi penggunaan material dan minimnya limbah produksi. Selain itu, pemahaman luas permukaan juga membantu dalam mendesain kemasan yang menarik dan fungsional.
Tabel Ringkasan Penerapan Luas Permukaan Prisma Segitiga
Tabel berikut merangkum contoh penerapan, manfaat, dan potensi kesulitan dalam perhitungan luas permukaan prisma segitiga.
| Contoh Penerapan | Manfaat Perhitungan | Potensi Kesulitan |
|---|---|---|
| Desain Rumah Kaca | Penghematan biaya material, struktur yang kokoh, efisiensi penggunaan material | Perhitungan yang kompleks jika bentuk rumah kaca tidak standar |
| Perencanaan Pembangunan Terowongan | Efisiensi biaya, konstruksi yang aman, perencanaan yang akurat | Pengukuran yang akurat pada lokasi proyek yang kompleks |
| Desain Kemasan Produk | Efisiensi penggunaan material, penghematan biaya produksi, desain kemasan yang optimal | Kompleksitas bentuk kemasan yang tidak standar |
Pengambilan Keputusan Berbasis Perhitungan Luas Permukaan Prisma Segitiga
Pengetahuan tentang luas permukaan prisma segitiga memungkinkan pengambilan keputusan yang lebih terinformasi dan efektif. Misalnya, dalam proyek konstruksi, perhitungan yang akurat akan mencegah pemborosan material dan biaya yang tidak perlu. Dalam desain produk, pemahaman ini membantu menciptakan desain yang efisien dan menarik. Dengan demikian, ketepatan perhitungan luas permukaan berdampak langsung pada efisiensi biaya, kualitas produk, dan keberhasilan proyek.
Ringkasan Akhir
Mempelajari contoh soal luas permukaan prisma segitiga tidak hanya sebatas menghafal rumus, tetapi juga memahami konsep dan aplikasinya dalam kehidupan nyata. Kemampuan menghitung luas permukaan prisma segitiga bermanfaat dalam berbagai bidang, mulai dari arsitektur hingga industri kemasan. Dengan latihan yang cukup dan pemahaman yang mendalam, kita dapat menguasai materi ini dengan baik dan siap menghadapi tantangan yang lebih kompleks.