Contoh soal statistika beserta jawabannya hadir untuk membantu Anda memahami konsep-konsep statistika secara lebih mendalam. Mulai dari statistika deskriptif yang membahas cara mendeskripsikan data, hingga statistika inferensial yang memungkinkan kita menarik kesimpulan dari sampel data, semua dijelaskan dengan contoh soal yang terstruktur dan mudah dipahami. Materi ini mencakup berbagai topik penting, seperti probabilitas, distribusi probabilitas, jenis-jenis data, dan representasi data, dilengkapi dengan penjelasan langkah demi langkah dalam penyelesaian soal.
Dengan beragam contoh soal yang meliputi perhitungan mean, median, modus, simpangan baku, varians, uji hipotesis, analisis regresi, dan ANOVA, Anda akan memiliki pemahaman yang komprehensif tentang penerapan statistika dalam berbagai konteks. Soal-soal yang disajikan dirancang untuk meningkatkan kemampuan analitis dan pemahaman konseptual Anda, sehingga Anda dapat mengaplikasikan statistika dalam kehidupan sehari-hari maupun dalam studi lanjut.
Pengantar Statistika Deskriptif

Statistika deskriptif merupakan cabang statistika yang berfokus pada penyajian dan interpretasi data. Perannya sangat penting karena memungkinkan kita untuk memahami pola, tren, dan karakteristik utama dari suatu kumpulan data tanpa perlu melakukan inferensi atau generalisasi ke populasi yang lebih besar. Dengan kata lain, statistika deskriptif membantu kita merangkum dan menyederhanakan informasi kompleks agar lebih mudah dipahami.
Statistika deskriptif digunakan secara luas dalam berbagai bidang, memungkinkan kita untuk mengambil kesimpulan yang bermakna dari data yang ada. Kemampuan untuk menganalisis dan menginterpretasikan data secara efektif merupakan keahlian yang berharga di berbagai profesi.
Penerapan Statistika Deskriptif dalam Kehidupan Sehari-hari
Statistika deskriptif berperan penting dalam berbagai aspek kehidupan sehari-hari. Misalnya, rata-rata nilai ujian siswa di sekolah dapat memberikan gambaran umum tentang prestasi akademik kelas tersebut. Laporan cuaca harian yang menampilkan suhu rata-rata, suhu tertinggi, dan terendah merupakan contoh lain dari penerapan statistika deskriptif. Begitu pula dengan survei kepuasan pelanggan yang menggunakan data untuk mengukur tingkat kepuasan pelanggan terhadap produk atau layanan suatu perusahaan.
Data tersebut kemudian disajikan dalam bentuk grafik atau tabel untuk memudahkan pemahaman.
Perbandingan Ukuran Pemusatan Data
Ukuran pemusatan data memberikan gambaran tentang nilai tengah dari suatu kumpulan data. Tiga ukuran pemusatan data yang umum digunakan adalah mean, median, dan modus. Ketiga ukuran ini memiliki karakteristik dan kegunaan yang berbeda, sehingga pilihan ukuran yang tepat bergantung pada jenis data dan tujuan analisis.
| Ukuran Pemusatan | Definisi | Kegunaan | Contoh |
|---|---|---|---|
| Mean (Rata-rata) | Jumlah semua nilai dibagi banyaknya nilai. | Cocok untuk data numerik yang terdistribusi normal. | Rata-rata nilai ujian siswa. |
| Median (Nilai Tengah) | Nilai tengah setelah data diurutkan. | Tahan terhadap outlier (nilai ekstrem). | Nilai tengah pendapatan rumah tangga. |
| Modus (Nilai yang Paling Sering Muncul) | Nilai yang paling sering muncul dalam data. | Cocok untuk data kategorik dan data numerik. | Ukuran sepatu yang paling banyak terjual. |
Contoh Perhitungan Mean, Median, dan Modus
Misalkan terdapat data nilai ujian sebagai berikut: 70, 80, 85, 90, 75, 80, 95.
Mean: (70 + 80 + 85 + 90 + 75 + 80 + 95) / 7 = 82,14
Median: Urutkan data terlebih dahulu: 70, 75, 80, 80, 85, 90, 95. Median adalah nilai tengah, yaitu 80.
Modus: Nilai yang paling sering muncul adalah 80.
Perhitungan Simpangan Baku dan Varians
Simpangan baku dan varians mengukur sebaran atau keragaman data di sekitar mean. Varians merupakan rata-rata kuadrat dari selisih antara setiap nilai data dengan mean. Simpangan baku adalah akar kuadrat dari varians. Nilai simpangan baku yang tinggi menunjukkan data yang tersebar luas, sedangkan nilai yang rendah menunjukkan data yang cenderung mengelompok di sekitar mean.
Mari kita hitung simpangan baku dan varians dari data nilai ujian sebelumnya (70, 80, 85, 90, 75, 80, 95). Mean-nya adalah 82,14.
Varians: Hitung selisih setiap nilai dengan mean, kuadratkan, jumlahkan, lalu bagi dengan jumlah data. Rumusnya adalah:
∑(xi – μ) 2 / N
Dimana x i adalah nilai data ke-i, μ adalah mean, dan N adalah jumlah data.
Setelah perhitungan, variansnya sekitar 102,39.
Simpangan Baku: Akar kuadrat dari varians. Jadi, simpangan baku adalah √102,39 ≈ 10,12.
Contoh Soal Statistika Inferensial

Statistika inferensial memungkinkan kita untuk menarik kesimpulan tentang populasi berdasarkan data sampel. Contoh soal berikut akan mengilustrasikan beberapa teknik inferensial yang umum digunakan, meliputi uji hipotesis satu dan dua pihak, analisis regresi linier sederhana, uji t untuk satu sampel, dan analisis varians (ANOVA) satu arah.
Uji Hipotesis Satu Pihak
Uji hipotesis satu pihak digunakan ketika kita memiliki hipotesis alternatif yang mengarah ke satu arah (lebih besar atau lebih kecil dari nilai tertentu). Contohnya, kita ingin menguji apakah rata-rata tinggi badan siswa di sekolah tertentu lebih dari 170 cm.
- Hipotesis Nol (H0): μ ≤ 170 cm
- Hipotesis Alternatif (H1): μ > 170 cm
- Sampel: Diambil sampel 30 siswa, dengan rata-rata tinggi badan 172 cm dan standar deviasi 5 cm.
- Tingkat signifikansi (α): 0.05
- Statistik uji: Uji t satu sampel akan digunakan untuk menguji hipotesis ini.
- Kesimpulan: Berdasarkan perhitungan uji t, kita dapat menentukan apakah cukup bukti untuk menolak hipotesis nol dan menyimpulkan bahwa rata-rata tinggi badan siswa lebih dari 170 cm.
Uji Hipotesis Dua Pihak
Uji hipotesis dua pihak digunakan ketika kita ingin menguji apakah terdapat perbedaan yang signifikan antara rata-rata dua kelompok atau antara rata-rata sampel dan nilai populasi yang diketahui, tanpa menentukan arah perbedaan tersebut. Sebagai contoh, kita ingin menguji apakah terdapat perbedaan signifikan antara rata-rata nilai ujian matematika siswa laki-laki dan perempuan.
- Hipotesis Nol (H0): μ laki-laki = μ perempuan
- Hipotesis Alternatif (H1): μ laki-laki ≠ μ perempuan
- Sampel: Diambil sampel 25 siswa laki-laki dengan rata-rata nilai 75 dan standar deviasi 10, dan 25 siswa perempuan dengan rata-rata nilai 78 dan standar deviasi 8.
- Tingkat signifikansi (α): 0.05
- Statistik uji: Uji t dua sampel independen akan digunakan.
- Kesimpulan: Berdasarkan hasil uji t, kita dapat menyimpulkan apakah terdapat perbedaan signifikan antara rata-rata nilai ujian matematika siswa laki-laki dan perempuan.
Analisis Regresi Linier Sederhana
Analisis regresi linier sederhana digunakan untuk memodelkan hubungan linier antara dua variabel. Misalnya, kita ingin memprediksi berat badan (Y) berdasarkan tinggi badan (X) seseorang.
- Data: Kita memiliki data tinggi badan dan berat badan dari sejumlah individu.
- Model: Model regresi linier sederhana berbentuk Y = β 0 + β 1X + ε, di mana β 0 adalah intercept, β 1 adalah slope, dan ε adalah error term.
- Estimasi Parameter: Kita akan menggunakan metode kuadrat terkecil untuk mengestimasi nilai β 0 dan β 1.
- Pengujian Signifikansi: Kita akan menguji signifikansi koefisien regresi (β 1) untuk melihat apakah hubungan antara tinggi badan dan berat badan signifikan secara statistik.
- Prediksi: Setelah model diestimasi, kita dapat menggunakannya untuk memprediksi berat badan seseorang berdasarkan tinggi badannya.
Langkah-langkah Penyelesaian Contoh Soal Uji t untuk Satu Sampel
Misalkan kita ingin menguji apakah rata-rata pendapatan bulanan karyawan di perusahaan tertentu berbeda secara signifikan dari Rp 5.000.000.
- Tentukan Hipotesis: H0: μ = 5.000.000; H1: μ ≠ 5.000.000
- Tentukan Tingkat Signifikansi: α = 0.05
- Kumpulkan Data Sampel: Misalnya, kita memiliki sampel 50 karyawan dengan rata-rata pendapatan Rp 5.200.000 dan standar deviasi Rp 800.000.
- Hitung Statistik Uji t: Rumus uji t satu sampel adalah:
t = (x̄
μ) / (s / √n)
dimana x̄ adalah rata-rata sampel, μ adalah rata-rata populasi, s adalah standar deviasi sampel, dan n adalah ukuran sampel.
- Tentukan Nilai Kritikal: Berdasarkan derajat bebas (n-1) dan tingkat signifikansi α, kita dapat menentukan nilai kritikal t dari tabel distribusi t.
- Buat Keputusan: Bandingkan nilai t hitung dengan nilai t kritikal. Jika nilai t hitung lebih besar dari nilai t kritikal (atau lebih kecil dari negatif nilai t kritikal), tolak H0.
Analisis Varian (ANOVA) Satu Arah
ANOVA satu arah digunakan untuk membandingkan rata-rata dari tiga kelompok atau lebih. Misalnya, kita ingin membandingkan efektivitas tiga jenis pupuk berbeda terhadap pertumbuhan tanaman.
- Data: Kita memiliki data tinggi tanaman untuk masing-masing jenis pupuk.
- Hipotesis: H0: Rata-rata tinggi tanaman untuk ketiga jenis pupuk sama; H1: Setidaknya satu rata-rata tinggi tanaman berbeda.
- Statistik Uji F: ANOVA menggunakan statistik uji F untuk membandingkan variansi antar kelompok dan variansi dalam kelompok.
- Kesimpulan: Berdasarkan nilai F hitung dan nilai F kritikal, kita dapat menentukan apakah terdapat perbedaan signifikan antara rata-rata tinggi tanaman untuk ketiga jenis pupuk.
Probabilitas dan Distribusi Probabilitas

Statistika seringkali berurusan dengan ketidakpastian. Probabilitas memberikan kerangka kerja untuk mengukur dan menganalisis ketidakpastian ini. Pemahaman tentang probabilitas dan berbagai distribusi probabilitas merupakan kunci untuk menginterpretasi data dan membuat kesimpulan yang bermakna. Berikut ini akan dijelaskan beberapa konsep kunci dan contoh penerapannya.
Konsep Probabilitas dan Contohnya
Probabilitas merupakan ukuran kemungkinan suatu kejadian terjadi. Nilai probabilitas selalu berada antara 0 dan 1 (inklusif), di mana 0 menunjukkan kejadian yang tidak mungkin terjadi dan 1 menunjukkan kejadian yang pasti terjadi. Contoh dalam konteks statistika: misalnya, jika kita melempar koin yang seimbang sebanyak 100 kali, kita mengharapkan sekitar 50 kali muncul sisi angka dan 50 kali muncul sisi gambar.
Probabilitas munculnya sisi angka dalam sekali lemparan adalah 0.5 atau 50%.
Contoh Soal Distribusi Binomial, Contoh soal statistika beserta jawabannya
Distribusi binomial digunakan untuk memodelkan jumlah keberhasilan dalam sejumlah percobaan Bernoulli yang independen dan identik. Percobaan Bernoulli adalah percobaan dengan dua kemungkinan hasil: sukses atau gagal.
Contoh soal: Sebuah pabrik memproduksi bola lampu dengan tingkat kerusakan 5%. Jika diambil sampel acak sebanyak 10 bola lampu, berapakah probabilitas tepat 2 bola lampu yang rusak?
Penyelesaian: Kita dapat menggunakan rumus distribusi binomial untuk menghitung probabilitas ini. Dengan n=10 (jumlah percobaan), p=0.05 (probabilitas sukses/rusak), dan k=2 (jumlah keberhasilan/bola lampu rusak), kita dapat menghitung probabilitasnya. Perhitungan detail rumus binomial akan menghasilkan nilai probabilitas tertentu.
Contoh Soal Distribusi Normal
Distribusi normal, juga dikenal sebagai distribusi Gaussian, merupakan distribusi probabilitas kontinu yang berbentuk lonceng simetris. Banyak fenomena alam dan data statistik mengikuti distribusi normal, atau setidaknya dapat didekati dengan distribusi normal.
Contoh soal: Tinggi badan siswa di suatu sekolah berdistribusi normal dengan rata-rata 170 cm dan simpangan baku 10 cm. Berapakah probabilitas seorang siswa yang dipilih secara acak memiliki tinggi badan antara 160 cm dan 180 cm?
Penyelesaian: Untuk menyelesaikan soal ini, kita perlu menstandarkan nilai tinggi badan menggunakan nilai z-score dan kemudian menggunakan tabel distribusi normal standar untuk mencari probabilitas yang diinginkan. Perhitungan akan melibatkan transformasi nilai tinggi badan ke dalam nilai z-score dan kemudian mencari luas area di bawah kurva distribusi normal antara dua nilai z-score tersebut.
Langkah-langkah Menyelesaikan Contoh Soal Distribusi Poisson
Distribusi Poisson digunakan untuk memodelkan jumlah kejadian yang terjadi dalam suatu interval waktu atau ruang tertentu, jika kejadian tersebut terjadi secara independen dan dengan rata-rata yang konstan.
Contoh soal: Sebuah pusat layanan pelanggan menerima rata-rata 5 panggilan telepon per menit. Berapakah probabilitas pusat layanan menerima tepat 3 panggilan telepon dalam satu menit?
- Tentukan parameter λ (lambda), yaitu rata-rata kejadian per unit waktu atau ruang. Dalam kasus ini, λ = 5 panggilan per menit.
- Tentukan nilai k, yaitu jumlah kejadian yang ingin kita hitung probabilitasnya. Dalam kasus ini, k = 3 panggilan.
- Gunakan rumus distribusi Poisson: P(X=k) = (e-λ
λk) / k!, di mana e adalah konstanta Euler (sekitar 2.71828).
- Substitusikan nilai λ dan k ke dalam rumus dan hitung probabilitasnya.
Perbedaan Distribusi Normal dan Distribusi t
Distribusi normal diasumsikan memiliki varians populasi yang diketahui, sedangkan distribusi t digunakan ketika varians populasi tidak diketahui dan diestimasi dari sampel. Distribusi t memiliki ekor yang lebih tebal dibandingkan distribusi normal, yang berarti distribusi t lebih rentan terhadap nilai ekstrem. Ketika ukuran sampel besar (biasanya lebih dari 30), distribusi t mendekati distribusi normal.
Jenis-jenis Data dan Pengukurannya
Dalam statistika, memahami jenis data sangat krusial karena metode analisis yang digunakan bergantung pada skala pengukuran datanya. Pengelompokan data berdasarkan skala pengukuran ini membantu kita memilih teknik analisis yang tepat dan menghasilkan interpretasi yang akurat. Berikut penjelasan mengenai jenis-jenis data dan contohnya.
Jenis-jenis Data
Data diklasifikasikan menjadi empat skala pengukuran utama: nominal, ordinal, interval, dan rasio. Perbedaan utama terletak pada sifat data dan operasi matematika yang dapat diterapkan padanya.
- Data Nominal: Data nominal hanya berfungsi untuk mengkategorikan atau mengelompokkan data tanpa urutan atau peringkat. Contohnya: jenis kelamin (laki-laki, perempuan), warna mata (hitam, coklat, biru), agama.
- Data Ordinal: Data ordinal memiliki urutan atau peringkat, tetapi selisih antar peringkat tidak memiliki makna kuantitatif yang pasti. Contohnya: tingkat kepuasan (sangat puas, puas, netral, tidak puas, sangat tidak puas), peringkat prestasi (pertama, kedua, ketiga), skala Likert.
- Data Interval: Data interval memiliki urutan dan selisih antar nilai yang bermakna, tetapi tidak memiliki titik nol absolut. Contohnya: suhu dalam Celcius atau Fahrenheit, tahun.
- Data Rasio: Data rasio memiliki urutan, selisih yang bermakna, dan titik nol absolut. Contohnya: tinggi badan, berat badan, pendapatan, usia.
Contoh Soal Data Nominal
Sebuah survei dilakukan kepada 100 responden mengenai warna mobil kesukaan mereka. Hasilnya adalah sebagai berikut: merah (30), biru (25), hitam (20), putih (15), hijau (10). Buatlah diagram lingkaran yang menggambarkan proporsi warna mobil kesukaan responden.
Penjelasan: Data warna mobil merupakan data nominal karena hanya menunjukkan kategori tanpa urutan tertentu. Diagram lingkaran cocok digunakan untuk memvisualisasikan proporsi data kategori.
Contoh Soal Data Ordinal
Sebuah restoran ingin mengetahui tingkat kepuasan pelanggan terhadap pelayanannya. Mereka menggunakan skala Likert dengan pilihan jawaban: Sangat Puas (5), Puas (4), Netral (3), Tidak Puas (2), Sangat Tidak Puas (1). Dari 50 pelanggan, 10 memilih Sangat Puas, 20 memilih Puas, 15 memilih Netral, 3 memilih Tidak Puas, dan 2 memilih Sangat Tidak Puas. Hitunglah frekuensi dan persentase setiap kategori tingkat kepuasan.
Penjelasan: Tingkat kepuasan merupakan data ordinal karena memiliki urutan peringkat, namun selisih antara “Sangat Puas” dan “Puas” tidak memiliki makna kuantitatif yang sama dengan selisih antara “Puas” dan “Netral”.
Contoh Soal Data Interval
Suhu rata-rata harian di kota X selama 5 hari berturut-turut adalah 25°C, 28°C, 26°C, 24°C, dan 27°C. Hitunglah suhu rata-rata harian selama 5 hari tersebut.
Penjelasan: Suhu dalam Celcius merupakan data interval karena memiliki urutan dan selisih yang bermakna, tetapi 0°C bukan berarti tidak ada suhu sama sekali.
Contoh Soal Data Rasio
Berat badan 5 orang siswa adalah 50 kg, 60 kg, 55 kg, 65 kg, dan 52 kg. Hitunglah berat badan rata-rata dan berat badan median kelima siswa tersebut.
Penjelasan: Berat badan merupakan data rasio karena memiliki urutan, selisih yang bermakna, dan titik nol absolut (0 kg berarti tidak ada berat badan).
Representasi Data
Representasi data merupakan langkah krusial dalam statistika. Visualisasi data yang tepat memungkinkan kita untuk memahami pola, tren, dan hubungan antar variabel dengan lebih efektif daripada sekadar melihat data mentah. Berikut beberapa contoh representasi data yang umum digunakan beserta penerapannya.
Pemilihan metode visualisasi bergantung pada jenis data dan informasi yang ingin disampaikan. Metode yang tepat akan memberikan gambaran yang jelas dan mudah dipahami.
Histogram
Histogram digunakan untuk menampilkan distribusi frekuensi data numerik. Data dikelompokkan ke dalam interval kelas, dan tinggi batang mewakili frekuensi data dalam setiap interval tersebut.
Contoh: Misalkan terdapat data nilai ujian 20 siswa sebagai berikut: 70, 75, 80, 80, 85, 85, 85, 90, 90, 90, 90, 95, 95, 95, 100, 100, 100, 100, 100, 100. Histogram akan menunjukkan sebaran nilai ujian tersebut, misalnya dengan interval kelas 70-79, 80-89, 90-99, dan 100-109. Batang yang paling tinggi akan berada pada interval kelas 100-109, menunjukkan bahwa banyak siswa mendapatkan nilai di rentang tersebut.
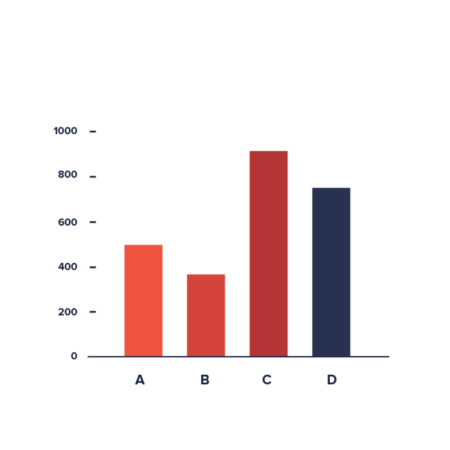
Diagram Batang
Diagram batang digunakan untuk membandingkan data kategorik atau data numerik diskrit. Panjang batang mewakili nilai data masing-masing kategori.
Contoh: Misalkan terdapat data jumlah penjualan produk A, B, dan C selama sebulan, yaitu 100 unit, 150 unit, dan 200 unit. Diagram batang akan menampilkan tiga batang dengan panjang yang berbeda, mewakili jumlah penjualan masing-masing produk. Perbandingan penjualan antar produk akan terlihat jelas.
Diagram Lingkaran
Diagram lingkaran digunakan untuk menunjukkan proporsi atau persentase dari keseluruhan data. Besar setiap irisan lingkaran mewakili proporsi dari setiap kategori.
Contoh: Misalkan terdapat data mengenai preferensi warna dari 100 responden, yaitu 30 responden menyukai merah, 40 responden menyukai biru, dan 30 responden menyukai hijau. Diagram lingkaran akan menunjukkan tiga irisan dengan ukuran yang berbeda, mewakili proporsi responden yang menyukai masing-masing warna. Sekilas terlihat bahwa warna biru paling banyak dipilih.
Box Plot
Box plot, atau diagram kotak, menampilkan ringkasan statistik dari data, termasuk median, kuartil pertama dan ketiga, serta nilai ekstrem (outlier). Box plot sangat berguna untuk membandingkan distribusi data dari beberapa kelompok.
Contoh: Misalkan terdapat data nilai ujian dua kelas yang berbeda. Box plot akan menunjukkan median, rentang interkuartil (IQR), dan outlier dari masing-masing kelas. Perbandingan antara kedua box plot akan memberikan gambaran mengenai perbedaan distribusi nilai ujian antara kedua kelas tersebut.
Visualisasi Data Lainnya
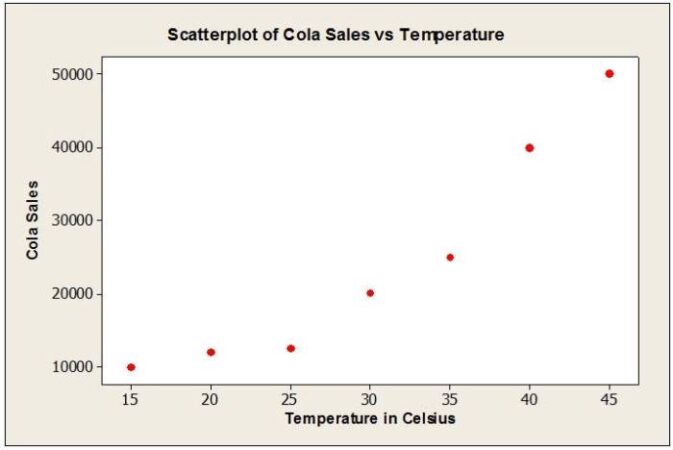
Selain histogram, diagram batang, diagram lingkaran, dan box plot, terdapat berbagai metode visualisasi data lainnya yang dapat digunakan, tergantung pada jenis data dan tujuan analisis. Beberapa contohnya adalah scatter plot (untuk melihat hubungan antara dua variabel numerik), peta panas (untuk menampilkan data dalam bentuk warna), dan jaringan (untuk menampilkan hubungan antara berbagai entitas).
Scatter plot misalnya, sangat berguna untuk melihat korelasi antara dua variabel. Jika titik-titik pada scatter plot membentuk pola garis lurus yang menanjak, hal ini mengindikasikan korelasi positif. Sebaliknya, jika membentuk garis lurus menurun, maka korelasi negatif. Peta panas efektif untuk menunjukkan variasi data geografis, misalnya kepadatan penduduk atau distribusi suhu.
Akhir Kata: Contoh Soal Statistika Beserta Jawabannya
Memahami statistika merupakan kunci untuk menganalisis data dan mengambil keputusan yang tepat. Melalui contoh soal statistika beserta jawabannya yang telah diuraikan, diharapkan Anda dapat mengasah kemampuan dalam mengolah dan menginterpretasi data secara efektif. Dengan latihan yang konsisten dan pemahaman yang mendalam terhadap konsep-konsep dasar, Anda akan mampu menghadapi tantangan analisa data dengan lebih percaya diri. Semoga contoh soal ini bermanfaat dalam perjalanan belajar Anda.