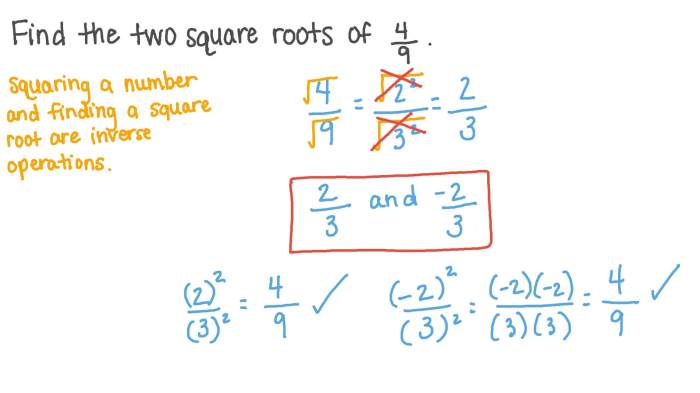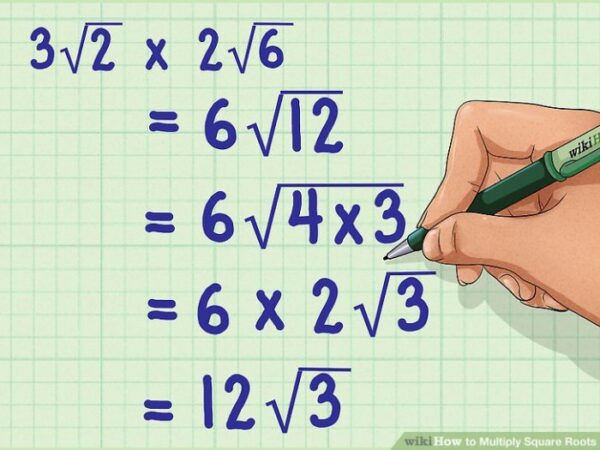- Pengertian Menyederhanakan Bentuk Akar
-
Metode Menyederhanakan Bentuk Akar
- Metode-Metode Menyederhanakan Bentuk Akar
- Penyederhanaan Bentuk Akar dengan Faktorisasi Prima
- Penyederhanaan Bentuk Akar yang Mengandung Pecahan
- Penyederhanaan Bentuk Akar yang Melibatkan Operasi Penjumlahan dan Pengurangan
- Contoh Soal dan Penyelesaian yang Menggunakan Kombinasi Metode, Soal menyederhanakan bentuk akar
- Menyederhanakan Bentuk Akar dengan Variabel: Soal Menyederhanakan Bentuk Akar
- Penerapan Menyederhanakan Bentuk Akar
- Penutupan Akhir
Soal menyederhanakan bentuk akar merupakan topik penting dalam matematika yang seringkali muncul dalam berbagai konteks, mulai dari geometri hingga fisika. Memahami cara menyederhanakan bentuk akar tidak hanya membantu dalam menyelesaikan soal-soal matematika, tetapi juga meningkatkan pemahaman konsep dasar aljabar. Artikel ini akan membahas secara detail berbagai metode dan penerapannya, mulai dari pengertian dasar hingga soal-soal yang lebih menantang.
Kita akan menjelajahi berbagai metode penyederhanaan, termasuk faktorisasi prima, penyederhanaan bentuk akar dengan pecahan dan variabel, serta penerapannya dalam pemecahan masalah geometri dan fisika. Dengan contoh-contoh soal yang terstruktur dan penjelasan langkah demi langkah, diharapkan pemahaman Anda tentang penyederhanaan bentuk akar akan semakin komprehensif dan tertanam kuat.
Pengertian Menyederhanakan Bentuk Akar
Menyederhanakan bentuk akar merupakan proses mengubah bentuk akar sedemikian rupa sehingga bentuknya lebih sederhana dan mudah dipahami. Proses ini melibatkan manipulasi aljabar untuk menghilangkan akar dari penyebut, menyederhanakan angka di dalam akar, atau menggabungkan akar-akar sejenis. Tujuan utama penyederhanaan ini adalah untuk mendapatkan representasi yang lebih efisien dan mudah diinterpretasi dari suatu bilangan irasional yang dinyatakan dalam bentuk akar.
Bentuk Akar Sederhana dan Belum Sederhana
Bentuk akar sederhana ditandai dengan tidak adanya faktor kuadrat sempurna di dalam tanda akar dan tidak adanya akar pada penyebut pecahan. Sebaliknya, bentuk akar yang belum sederhana memuat faktor kuadrat sempurna di dalam tanda akar atau memiliki akar pada penyebut pecahan. Perbedaan ini berpengaruh pada kemudahan dalam perhitungan dan pemahaman nilai bilangan tersebut.
Contoh bentuk akar sederhana: √2, 3√5, 2√
7. Contoh bentuk akar yang belum sederhana: √12 (karena 12 = 4 x 3, dan 4 adalah kuadrat sempurna), √(18/25) (karena terdapat akar pada penyebut).
Langkah-langkah Menyederhanakan Bentuk Akar
Secara umum, menyederhanakan bentuk akar melibatkan beberapa langkah. Langkah-langkah ini membantu untuk memperoleh bentuk akar yang paling sederhana dan efisien.
- Mencari faktor kuadrat sempurna: Identifikasi faktor-faktor kuadrat sempurna (misalnya, 4, 9, 16, 25, dst.) yang merupakan faktor dari bilangan di dalam tanda akar.
- Menguraikan bilangan dalam tanda akar: Uraikan bilangan di dalam tanda akar menjadi perkalian antara faktor kuadrat sempurna dan faktor lainnya.
- Menyederhanakan akar kuadrat sempurna: Akar kuadrat dari faktor kuadrat sempurna dapat disederhanakan menjadi bilangan bulat.
- Merasionalkan penyebut (jika ada): Jika terdapat akar pada penyebut pecahan, kalikan pembilang dan penyebut dengan akar sekawan penyebut untuk menghilangkan akar pada penyebut.
Contoh Soal dan Penyelesaian
Berikut adalah contoh soal yang menunjukkan proses menyederhanakan bentuk akar:
| Bentuk Akar Belum Sederhana | Penyelesaian | Bentuk Akar Sederhana |
|---|---|---|
| √75 | √(25 x 3) = √25 x √3 = 5√3 | 5√3 |
| √(18/8) | √(9 x 2 / 4 x 2) = (√9 x √2) / (√4 x √2) = (3√2) / (2√2) = 3/2 | 3/2 |
| 3√2 + 5√2 | (3+5)√2 = 8√2 | 8√2 |
Metode Menyederhanakan Bentuk Akar

Menyederhanakan bentuk akar merupakan proses penting dalam aljabar untuk mendapatkan bentuk paling sederhana dari suatu bilangan irasional yang mengandung akar. Proses ini melibatkan beberapa metode, dan pemahaman akan metode-metode tersebut akan memudahkan dalam menyelesaikan berbagai soal matematika yang melibatkan bentuk akar.
Metode-Metode Menyederhanakan Bentuk Akar
Berikut beberapa metode yang umum digunakan dalam menyederhanakan bentuk akar, beserta contoh penerapannya:
| Metode | Penjelasan | Contoh | Hasil |
|---|---|---|---|
| Faktorisasi Prima | Mencari faktor prima dari bilangan di dalam akar dan mengelompokkan faktor-faktor yang berpasangan. | √12 | 2√3 (karena 12 = 2 x 2 x 3) |
| Menggunakan Sifat Akar | Menggunakan sifat √(a x b) = √a x √b dan √(a/b) = √a / √b untuk menyederhanakan bentuk akar. | √(4/9) | 2/3 (karena √4 = 2 dan √9 = 3) |
| Rasionalisasi | Mengalikan pembilang dan penyebut dengan bentuk akar sekawan untuk menghilangkan akar pada penyebut. | 2/√3 | (2√3)/3 (dikalikan dengan √3/√3) |
| Menggunakan Identitas Aljabar | Menggunakan identitas aljabar seperti (a+b)(a-b) = a²
|
√(x²-4) | Tidak dapat disederhanakan lebih lanjut tanpa informasi tambahan tentang nilai x. |
Penyederhanaan Bentuk Akar dengan Faktorisasi Prima
Metode faktorisasi prima merupakan salah satu metode yang paling dasar dan sering digunakan. Langkah-langkahnya adalah sebagai berikut:
- Faktorkan bilangan di dalam tanda akar menjadi faktor-faktor prima.
- Kelompokkan faktor-faktor prima yang berpasangan.
- Keluarkan pasangan faktor prima dari dalam tanda akar.
- Sederhanakan bentuk akar yang tersisa.
Contoh: Sederhanakan √72. 72 difaktorkan menjadi 2 x 2 x 2 x 3 x 3. Pasangan 2 dan 3 dikeluarkan dari akar, sehingga hasilnya adalah 6√2.
Penyederhanaan Bentuk Akar yang Mengandung Pecahan
Penyederhanaan bentuk akar yang mengandung pecahan dapat dilakukan dengan merasionalkan penyebut atau dengan menyederhanakan pembilang dan penyebut secara terpisah.
Contoh: Sederhanakan √(12/25). Bentuk ini dapat disederhanakan menjadi √12 / √25 = (2√3)/5
Penyederhanaan Bentuk Akar yang Melibatkan Operasi Penjumlahan dan Pengurangan
Untuk menyederhanakan bentuk akar yang melibatkan penjumlahan dan pengurangan, pertama-tama sederhanakan setiap bentuk akar terlebih dahulu. Setelah itu, baru lakukan operasi penjumlahan atau pengurangan. Pastikan bahwa bentuk akar yang dijumlahkan atau dikurangkan memiliki bagian dalam akar yang sama.
Contoh: Sederhanakan 2√3 + √12 – √27. √12 = 2√3 dan √27 = 3√3. Maka, persamaan menjadi 2√3 + 2√3 – 3√3 = √3.
Contoh Soal dan Penyelesaian yang Menggunakan Kombinasi Metode, Soal menyederhanakan bentuk akar
Sederhanakan √(48/27) + 2√3 – √75.
- Sederhanakan √(48/27): 48 = 24 x 3 dan 27 = 3 3. Maka √(48/27) = √(16/9) x √3 = (4/3)√3
- Sederhanakan √75: 75 = 5 2 x 3. Maka √75 = 5√3
- Substitusikan ke persamaan awal: (4/3)√3 + 2√3 – 5√3 = (4/3 + 2 – 5)√3 = (-5/3)√3
Menyederhanakan Bentuk Akar dengan Variabel: Soal Menyederhanakan Bentuk Akar

Menyederhanakan bentuk akar yang melibatkan variabel membutuhkan pemahaman yang baik tentang sifat-sifat akar dan operasi aljabar. Prosesnya mirip dengan menyederhanakan bentuk akar tanpa variabel, namun kita perlu memperhatikan pangkat variabel dan aturan eksponen.
Bentuk Akar dengan Variabel Pangkat Dua
Penyederhanaan bentuk akar dengan variabel pangkat dua bergantung pada pengelompokan faktor-faktor yang membentuk kuadrat sempurna. Kita dapat mengeluarkan faktor-faktor tersebut dari dalam akar kuadrat.
Contoh: Sederhanakan √(16x²).
Penyelesaian: √(16x²) = √(16)
– √(x²) = 4x. (Asumsi x ≥ 0)
Contoh lain: Sederhanakan √(27x²y⁴).
Penyelesaian: √(27x²y⁴) = √(9
– 3
– x²
– y⁴) = √(9)
– √(3)
– √(x²)
– √(y⁴) = 3xy²√3. (Asumsi x ≥ 0 dan y ≥ 0)
Bentuk Akar dengan Variabel Pangkat Tiga
Penyederhanaan bentuk akar pangkat tiga (akar kubik) melibatkan pengelompokan faktor-faktor yang membentuk kubus sempurna. Faktor-faktor ini kemudian dikeluarkan dari akar kubik.
Contoh: Sederhanakan ³√(8x³).
Penyelesaian: ³√(8x³) = ³√(8)
– ³√(x³) = 2x.
Contoh lain: Sederhanakan ³√(27x⁶y⁹).
Penyelesaian: ³√(27x⁶y⁹) = ³√(27)
– ³√(x⁶)
– ³√(y⁹) = 3x²y³
Bentuk Akar dengan Variabel dan Konstanta
Penyederhanaan bentuk akar yang melibatkan variabel dan konstanta menggabungkan teknik-teknik yang telah dijelaskan sebelumnya. Kita perlu mengidentifikasi faktor-faktor yang merupakan kuadrat sempurna atau kubus sempurna, baik berupa konstanta maupun variabel.
Contoh: Sederhanakan √(12x²y).
Penyelesaian: √(12x²y) = √(4
– 3
– x²
– y) = √(4)
– √(3)
– √(x²)
– √(y) = 2x√(3y). (Asumsi x ≥ 0 dan y ≥ 0)
Contoh Soal Menantang
Sederhanakan √(75a⁴b³c) + √(12a²bc)
-√(48a⁴b³c) , dengan asumsi a, b, c ≥ 0.
Penyelesaian:
- √(75a⁴b³c) = √(25
- 3
- a⁴
- b²
- b
- c) = 5a²b√(3bc)
- √(12a²bc) = √(4
- 3
- a²
- b
- c) = 2a√(3bc)
- √(48a⁴b³c) = √(16
- 3
- a⁴
- b²
- b
- c) = 4a²b√(3bc)
Maka, √(75a⁴b³c) + √(12a²bc)
-√(48a⁴b³c) = 5a²b√(3bc) + 2a√(3bc)
-4a²b√(3bc) = (5a²b – 4a²b + 2a)√(3bc) = (a²b + 2a)√(3bc).
Penerapan Menyederhanakan Bentuk Akar
Setelah memahami teknik menyederhanakan bentuk akar, penting untuk melihat penerapannya dalam berbagai bidang, khususnya dalam pemecahan masalah matematika dan ilmu terapan seperti geometri dan fisika. Kemampuan ini memungkinkan kita untuk mendapatkan hasil yang lebih akurat dan efisien, serta memahami konsep-konsep matematis dengan lebih baik.
Penerapan dalam Geometri: Menghitung Panjang Sisi Segitiga
Penyederhanaan bentuk akar sangat berguna dalam geometri, terutama saat menghitung panjang sisi segitiga. Misalnya, perhatikan segitiga siku-siku dengan panjang sisi tegak 3 cm dan 4 cm. Dengan teorema Pythagoras, panjang sisi miring (hipotenusa) adalah √(3² + 4²) = √25 = 5 cm. Namun, jika panjang sisi tegak adalah 2 cm dan 3 cm, maka panjang sisi miring adalah √(2² + 3²) = √13 cm.
Bentuk √13 ini sudah dalam bentuk paling sederhana dan memberikan nilai yang tepat untuk panjang sisi miring. Tanpa penyederhanaan bentuk akar, kita hanya akan mendapatkan nilai pendekatan, yang mungkin kurang akurat untuk keperluan tertentu.
Penerapan dalam Perhitungan Luas Bangun Datar
Perhitungan luas bangun datar juga sering melibatkan bentuk akar. Bayangkan sebuah segitiga sama sisi dengan panjang sisi 2√3 cm. Luas segitiga sama sisi dapat dihitung dengan rumus ½ x sisi x tinggi. Tinggi segitiga sama sisi dapat dihitung dengan rumus ½ x sisi x √3. Dalam kasus ini, tinggi segitiga adalah ½ x 2√3 cm x √3 = 3 cm.
Luas segitiga tersebut adalah ½ x 2√3 cm x 3 cm = 3√3 cm². Dengan menyederhanakan bentuk akar, kita memperoleh hasil yang tepat dan sederhana. Jika kita tidak menyederhanakan √12 menjadi 2√3, perhitungan luas akan menjadi lebih rumit dan hasilnya kurang efisien.
Penerapan dalam Fisika
Dalam fisika, penyederhanaan bentuk akar sering digunakan dalam perhitungan yang melibatkan vektor dan kecepatan. Misalnya, perhatikan sebuah objek yang bergerak dengan kecepatan 4 m/s ke arah timur dan 3 m/s ke arah utara. Kecepatan resultan objek tersebut dapat dihitung menggunakan teorema Pythagoras: √(4² + 3²) = √25 = 5 m/s. Penyederhanaan bentuk akar memastikan perhitungan yang akurat dan efisien dalam menentukan kecepatan resultan.
Pentingnya Menyederhanakan Bentuk Akar dalam Pemecahan Masalah Matematika
Kemampuan menyederhanakan bentuk akar merupakan keterampilan dasar dalam matematika yang sangat penting untuk menyelesaikan berbagai macam masalah. Hal ini memungkinkan kita untuk mendapatkan hasil yang lebih akurat, efisien, dan mudah dipahami. Selain itu, penguasaan teknik ini juga mempermudah dalam melakukan perhitungan lebih lanjut dan memahami konsep-konsep matematika yang lebih kompleks.
Penyederhanaan bentuk akar merupakan kunci untuk mendapatkan hasil yang akurat dan efisien dalam berbagai perhitungan matematis dan ilmu terapan. Kemampuan ini sangat penting dalam geometri, fisika, dan berbagai bidang lainnya yang melibatkan perhitungan yang kompleks.
Penutupan Akhir

Menyederhanakan bentuk akar merupakan keterampilan penting dalam matematika yang memiliki aplikasi luas di berbagai bidang. Dengan memahami berbagai metode dan teknik yang telah dijelaskan, diharapkan pembaca dapat dengan mudah menyelesaikan berbagai soal yang melibatkan bentuk akar, baik yang sederhana maupun yang kompleks. Kemampuan ini tidak hanya akan membantu dalam memecahkan masalah matematika, tetapi juga akan meningkatkan pemahaman konseptual dan kemampuan berpikir analitis secara keseluruhan.