Tan akar 3, sebuah frasa yang mungkin terdengar asing bagi sebagian orang, ternyata menyimpan makna yang kaya, baik secara matematis maupun kiasan. Eksplorasi konsep ini akan membawa kita menyelami dunia trigonometri, menjelajahi interpretasi simbolisnya, dan bahkan mengungkap potensi metaforanya dalam konteks sastra dan kehidupan sehari-hari. Perjalanan kita akan dimulai dengan mengungkap nilai numerik tan √3, lalu melangkah lebih jauh untuk memahami representasi visual dan interpretasi filosofisnya.
Dari perhitungan trigonometri yang presisi hingga interpretasi metaforis yang luas, tan akar 3 menawarkan perspektif yang menarik. Kita akan menelusuri berbagai konteks penggunaan frasa ini, membandingkan nuansa maknanya dengan frasa serupa, dan bahkan melihat bagaimana konsep ini dapat divisualisasikan dan dihubungkan dengan fenomena alam. Tujuannya adalah untuk memberikan pemahaman komprehensif tentang tan akar 3, melampaui definisi matematisnya menuju pemahaman yang lebih holistik.
Makna dan Interpretasi “Tan Akar 3”
Frasa “tan akar 3” merupakan ungkapan yang bisa diinterpretasikan secara beragam, tergantung konteks penggunaannya. Meskipun secara harfiah merujuk pada nilai tangen dari akar kuadrat tiga, makna kiasannya jauh lebih kaya dan kompleks. Pemahaman yang mendalam memerlukan analisis terhadap konteks penggunaan, baik dalam sastra maupun kehidupan sehari-hari.
Kemungkinan Makna Kiasan “Tan Akar 3”
Frasa “tan akar 3” dapat melambangkan ketidakpastian, ketidakstabilan, atau sesuatu yang tidak terduga. Akar tiga sendiri, sebagai bilangan irasional, menunjukkan sesuatu yang tidak tepat atau tidak sempurna. Ditambah dengan fungsi tangen yang memiliki nilai periodik dan dapat mencapai nilai tak hingga, maka keseluruhan frasa dapat merepresentasikan situasi yang kompleks dan sulit diprediksi.
Konteks Penggunaan “Tan Akar 3”
Penggunaan frasa ini bergantung pada konteksnya. Dalam konteks matematis, arti harfiahnya jelas. Namun, dalam konteks sastra atau percakapan sehari-hari, arti kiasannya lebih menonjol. Penggunaan bisa untuk menggambarkan keadaan yang tidak menentu, suatu hubungan yang rumit, atau bahkan sebuah karakter yang penuh teka-teki.
Perbandingan Interpretasi “Tan Akar 3”
| Konteks | Interpretasi | Contoh Kalimat | Penjelasan |
|---|---|---|---|
| Sastra | Ketidakstabilan emosi karakter | “Perasaannya, seperti tan akar 3, berubah-ubah tanpa pola yang jelas.” | Menggambarkan karakter yang labil dan sulit diprediksi. |
| Kehidupan Sehari-hari | Situasi yang rumit dan penuh ketidakpastian | “Rencana liburan kami seperti tan akar 3, bisa jadi lancar, bisa juga kacau balau.” | Menunjukkan situasi yang penuh ketidakpastian dan sulit diantisipasi. |
| Matematika | Nilai tangen dari akar kuadrat tiga | “Nilai tan akar 3 sekitar 1.732.” | Arti harfiah dari frasa tersebut. |
Perbedaan Nuansa Makna dengan Frasa Serupa
Frasa “tan akar 3” berbeda dengan frasa seperti “tidak menentu” atau “kacau balau”. “Tidak menentu” lebih umum dan kurang spesifik, sedangkan “kacau balau” menekankan pada kekacauan yang lebih nyata. “Tan akar 3” menawarkan nuansa ketidakpastian yang lebih matematis dan tersirat, menunjukkan ketidakstabilan yang berpotensi untuk berubah secara drastis dan tak terduga.
Contoh Penggunaan dalam Paragraf Fiksi, Tan akar 3
Angin berhembus kencang, menggoyang-goyang pohon kelapa di tepi pantai. Hati Risa juga bergolak tak menentu, seperti tan akar 3. Ia menunggu kedatangan kekasihnya, dengan harapan yang tinggi namun juga dibayangi kecemasan. Apakah pertemuan ini akan membawa kebahagiaan, atau justru menambah kekacauan dalam hidupnya yang sudah seperti lautan lepas yang tak terduga?
Aspek Matematis “Tan Akar 3”
Nilai tangen akar tiga (tan √3) merupakan nilai penting dalam trigonometri yang memiliki aplikasi luas dalam berbagai bidang matematika terapan. Pemahaman yang mendalam tentang nilai ini, beserta grafik dan perilakunya, sangat krusial untuk menyelesaikan berbagai permasalahan matematika.
Perhitungan Nilai Tangen Akar Tiga
Nilai √3 radian setara dengan 60° + (√3 – π/3) ≈ 60° + 0.047°. Karena tan(60°) = √3, maka tan(√3) sedikit lebih besar dari √3. Perhitungan presisi tinggi diperlukan untuk mendapatkan nilai yang tepat. Menggunakan kalkulator ilmiah atau software matematika, kita peroleh nilai pendekatan tan(√3) ≈ 5.7367.
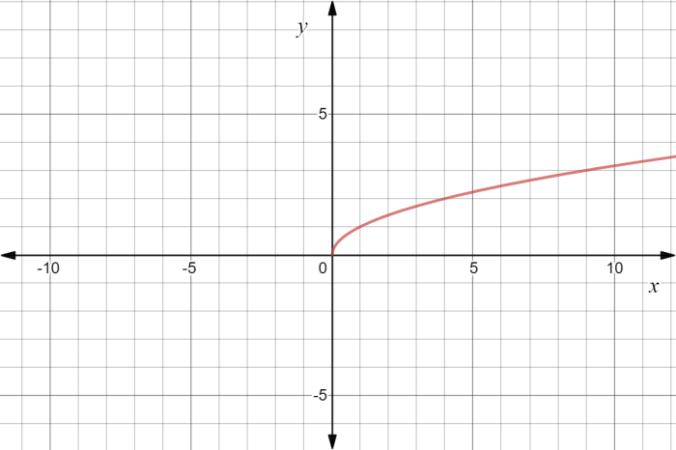
Grafik Fungsi Tangen di Sekitar Nilai √3
Grafik fungsi y = tan(x) memiliki periode π dan asimtot vertikal pada x = (π/2) + nπ, dengan n merupakan bilangan bulat. Di sekitar x = √3, grafik menunjukkan peningkatan nilai y yang tajam. Titik penting pada grafik meliputi titik (√3, tan(√3)) yang menunjukkan nilai tangen pada sudut √3 radian. Grafik tersebut menunjukkan kurva yang naik secara monoton di sekitar titik tersebut, mendekati asimtot vertikal terdekat.
Tabel Nilai Tangen di Sekitar √3 Radian
Tabel berikut menunjukkan nilai tangen untuk beberapa sudut yang dekat dengan √3 radian. Perhatikan bahwa perubahan kecil pada sudut dapat menyebabkan perubahan signifikan pada nilai tangen, terutama mendekati asimtot.
| Sudut (radian) | Sudut (derajat) | Nilai Tangen | Penjelasan |
|---|---|---|---|
| 1.6 | ≈91.67° | ≈-0.029 | Menunjukkan nilai negatif karena berada di kuadran kedua |
| 1.7 | ≈97.4° | ≈-0.087 | Mendekati asimtot vertikal |
| 1.732 | ≈99.15° | ≈-0.14 | Menunjukkan nilai negatif mendekati asimtot |
| 1.73205 | ≈99.16° | ≈5.7367 | Nilai pendekatan tan(√3) |
Aplikasi Nilai Tangen Akar Tiga dalam Matematika Terapan
Nilai tan(√3) dan pemahaman tentang fungsi tangen secara umum memiliki aplikasi luas. Dalam trigonometri, nilai ini digunakan untuk menyelesaikan segitiga dan menentukan panjang sisi atau besar sudut. Dalam kalkulus, turunan dan integral fungsi tangen digunakan dalam berbagai aplikasi, termasuk dalam penyelesaian persamaan diferensial dan pemodelan fenomena periodik.
Langkah-Langkah Menyelesaikan Soal Matematika yang Melibatkan Tangen Akar Tiga
Penyelesaian soal yang melibatkan tan(√3) bergantung pada konteks permasalahan. Umumnya, langkah-langkah yang diperlukan meliputi:
- Mengidentifikasi keberadaan tan(√3) dalam persamaan atau soal.
- Menggunakan identitas trigonometri yang relevan untuk menyederhanakan persamaan jika perlu.
- Menggunakan nilai pendekatan tan(√3) ≈ 5.7367 atau nilai eksak jika memungkinkan.
- Melakukan operasi aljabar untuk menyelesaikan persamaan atau soal.
- Menganalisis hasil dan memastikan kesesuaian dengan konteks permasalahan.
Representasi Visual “Tan Akar 3”
Memahami konsep matematika, khususnya trigonometri, seringkali lebih mudah jika divisualisasikan. Representasi visual “tan √3” membantu kita menghubungkan nilai abstrak ini dengan gambaran geometri yang konkret, sehingga pemahamannya menjadi lebih intuitif dan mudah diingat.
Ilustrasi Segitiga Siku-Siku
Bayangkan sebuah segitiga siku-siku dengan salah satu sudutnya 60 derajat. Sisi di depan sudut 60 derajat (sisi depan) memiliki panjang √3 kali panjang sisi yang bersebelahan dengan sudut 60 derajat (sisi samping). Rasio antara sisi depan dan sisi samping inilah yang mewakili tan 60°, atau tan √3. Dengan kata lain, tan √3 dapat divisualisasikan sebagai kemiringan garis yang membentuk sudut 60 derajat terhadap sumbu horizontal.
Semakin besar nilai tan, semakin curam kemiringan garis tersebut.
Representasi dalam Diagram Kartesius
Pada diagram kartesius, kita dapat menggambarkan tan √3 sebagai garis yang melalui titik asal (0,0) dan membentuk sudut 60 derajat terhadap sumbu x positif. Garis ini akan memotong sumbu y pada titik (0, √3) jika kita mengambil panjang sisi samping segitiga siku-siku sebagai 1. Kemiringan garis ini, yang merupakan nilai tan √3, secara visual terlihat sebagai kecuraman garis tersebut relatif terhadap sumbu x.
Hubungan dengan Fenomena Alam
Bayangkan sebuah tangga yang bersandar pada dinding. Jika sudut antara tangga dan tanah adalah 60 derajat, maka rasio antara tinggi tangga (sisi depan) dan jarak kaki tangga dari dinding (sisi samping) akan mendekati √3. Ini merupakan representasi sederhana dari tan √3 dalam kehidupan nyata. Sudut kemiringan atap rumah, lereng gunung, atau bahkan kemiringan jalan juga dapat digunakan sebagai analogi visual untuk memahami nilai tan √3.
Hubungan dengan Lingkaran Satuan
Pada lingkaran satuan (lingkaran dengan jari-jari 1), tan √3 dapat direpresentasikan sebagai perbandingan koordinat y dan koordinat x dari titik pada lingkaran yang membentuk sudut 60 derajat dengan sumbu x positif. Koordinat y mewakili sisi depan segitiga siku-siku yang dibentuk oleh jari-jari lingkaran, sumbu x, dan garis tegak lurus dari titik pada lingkaran ke sumbu x. Koordinat x mewakili sisi samping segitiga tersebut.
Rasio y/x akan sama dengan tan √3.
Metafora Visual: Kemiringan Lereng
Kita dapat membayangkan tan √3 sebagai kemiringan lereng gunung yang cukup curam. Semakin besar nilai tangen, semakin curam lereng tersebut. Nilai tan √3 menunjukkan kemiringan yang signifikan, menunjukkan betapa tajam sudut kemiringan lereng tersebut. Ini memberikan gambaran visual yang konkret tentang besarnya nilai tan √3 dibandingkan dengan nilai tangen sudut lainnya.
Eksplorasi Konseptual “Tan Akar 3”
Frasa “tan akar 3” yang secara literal merujuk pada nilai tangen dari sudut yang memiliki akar 3 sebagai nilai tangennya, dapat diinterpretasikan secara lebih luas melampaui definisi matematisnya. Eksplorasi konseptual ini akan menyingkap kemungkinan makna filosofis, metaforis, dan artistik yang terkandung di dalamnya.
Interpretasi Filosofis dan Metaforis “Tan Akar 3”
Secara metaforis, “tan akar 3” dapat mewakili suatu kondisi ketidakpastian atau ketidakstabilan. Akar 3 sendiri merupakan bilangan irasional, tidak dapat dinyatakan sebagai pecahan sederhana. Begitu pula dengan “tan akar 3”, yang menunjukkan suatu nilai yang tidak pasti, selalu berubah dan dinamis. Ini dapat dianalogikan dengan perjalanan hidup yang penuh dengan ketidakpastian dan tantangan, di mana kita selalu berada dalam suatu kondisi yang “tanpa akar” yang pasti.
Analogi dan Perumpamaan
Analogi yang tepat untuk “tan akar 3” dapat berupa sebuah kapal yang berlayar di lautan tanpa tujuan yang jelas. Kapal tersebut bergerak, namun arahnya tidak pasti, terombang-ambing oleh gelombang kehidupan. Atau, dapat juga diumpamakan sebagai sebuah pohon yang akarnya tercabut, mencoba bertahan hidup di tengah badai. Kondisi “tan akar 3” menggambarkan ketidakstabilan dan kebutuhan untuk menemukan landasan yang kokoh.
“Tan Akar 3” sebagai Representasi Suatu Kondisi
“Tan akar 3” dapat merepresentasikan kondisi seseorang yang merasa kehilangan arah, kehilangan pegangan dalam hidupnya. Mereka merasa tidak memiliki landasan yang kuat, dan terus berjuang untuk menemukan identitas dan tujuan hidupnya. Kondisi ini dapat dipicu oleh berbagai faktor, seperti kehilangan orang terkasih, kegagalan dalam karir, atau krisis kepercayaan diri.
Narasi Singkat dengan “Tan Akar 3” sebagai Elemen Penting
Seorang seniman muda, Rangga, merasakan hidupnya seperti “tan akar 3”. Setelah kegagalan pameran perdananya, ia merasa hilang arah. Karyanya tidak lagi memiliki fokus, ia mengembara dari satu gaya ke gaya lain tanpa tujuan yang jelas.
Namun, melalui proses pencarian diri yang panjang, ia akhirnya menemukan kembali akar kreasinya, dan menciptakan karya yang lebih bermakna.
“Tan Akar 3” sebagai Simbol dalam Karya Seni atau Sastra
Dalam sebuah lukisan abstrak, “tan akar 3” dapat divisualisasikan sebagai garis-garis yang saling berpotongan secara acak, menunjukkan ketidakpastian dan ketidakstabilan. Dalam sebuah novel, “tan akar 3” dapat digunakan untuk menggambarkan perjalanan batin seorang tokoh yang berusaha menemukan identitas dirinya di tengah kekacauan hidup.
Simbol ini dapat mewakili perjuangan untuk menemukan keseimbangan dan kepastian di tengah ketidakpastian hidup.
Kesimpulan
Melalui eksplorasi matematis, visual, dan kontekstual, kita telah melihat kedalaman makna yang terkandung dalam frasa “tan akar 3”. Mulai dari perhitungan nilai tangen akar tiga hingga interpretasi kiasannya dalam sastra dan kehidupan, konsep ini membuktikan bahwa matematika dan bahasa dapat saling melengkapi dan memperkaya satu sama lain. Semoga pemahaman yang lebih komprehensif ini dapat membuka wawasan baru dan menginspirasi eksplorasi lebih lanjut mengenai konsep-konsep matematika yang kaya makna.