- Menentukan Nilai x dalam Persamaan Sederhana
- Menentukan Nilai x dalam Persamaan Kuadrat: Tentukan Nilai X Serta Jelaskan Alasanmu
-
Menentukan Nilai x dalam Persamaan Linear Dua Variabel
- Penyelesaian Sistem Persamaan 2x + y = 7 dan x – y = 2
- Penyelesaian Sistem Persamaan x + 3y = 10 dan 2x – y = 5, Tentukan nilai x serta jelaskan alasanmu
- Perbandingan Metode Substitusi dan Eliminasi pada Sistem Persamaan 3x + 2y = 11 dan x – y = 2
- Penyelesaian Sistem Persamaan 4x – y = 9 dan x + 2y = 6
- Representasi Grafik Sistem Persamaan x + y = 5 dan x – y = 1
- Menentukan Nilai x dalam Persamaan Lainnya
- Penutup
Tentukan Nilai x serta Jelaskan Alasanmu; sebuah pertanyaan yang sering muncul dalam berbagai konteks matematika. Pemahaman mendalam tentang bagaimana menentukan nilai x sangat krusial, baik dalam persamaan sederhana maupun yang lebih kompleks seperti persamaan kuadrat atau sistem persamaan linear. Artikel ini akan membahas berbagai metode untuk menemukan nilai x, mulai dari persamaan linear sederhana hingga persamaan eksponensial dan logaritma, disertai penjelasan langkah demi langkah yang detail dan mudah dipahami.
Dari persamaan sederhana seperti 2x + 5 = 11 hingga persamaan kuadrat dan sistem persamaan linear dua variabel, kita akan menjelajahi berbagai teknik penyelesaian. Dengan memahami prinsip-prinsip dasar aljabar, kita dapat dengan mudah menentukan nilai x dan memahami alasan di balik setiap langkah perhitungan. Setiap contoh akan dilengkapi dengan penjelasan rinci, memastikan pemahaman yang menyeluruh tentang konsep yang dibahas.
Menentukan Nilai x dalam Persamaan Sederhana
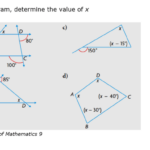
Menentukan nilai x dalam persamaan sederhana merupakan keterampilan dasar dalam aljabar. Kemampuan ini penting karena menjadi fondasi untuk menyelesaikan persamaan yang lebih kompleks. Dalam artikel ini, kita akan membahas langkah-langkah sistematis untuk menemukan nilai x dalam beberapa contoh persamaan sederhana, serta membandingkan beberapa metode penyelesaiannya.
Menentukan Nilai x dalam Persamaan 2x + 5 = 11
Untuk menentukan nilai x dalam persamaan 2x + 5 = 11, kita perlu mengisolasi variabel x. Langkah-langkahnya sebagai berikut:
- Kurangi 5 dari kedua ruas persamaan: 2x + 5 – 5 = 11 – 5 ⇒ 2x = 6
- Bagi kedua ruas persamaan dengan 2: 2x / 2 = 6 / 2 ⇒ x = 3
Jadi, nilai x yang memenuhi persamaan 2x + 5 = 11 adalah 3.
Menentukan Nilai x dalam Persamaan 3x – 7 = 8
Penyelesaian persamaan 3x – 7 = 8 dilakukan dengan langkah-langkah berikut:
- Tambahkan 7 ke kedua ruas persamaan: 3x – 7 + 7 = 8 + 7 ⇒ 3x = 15
- Bagi kedua ruas persamaan dengan 3: 3x / 3 = 15 / 3 ⇒ x = 5
Oleh karena itu, nilai x yang memenuhi persamaan 3x – 7 = 8 adalah 5.
Menentukan Nilai x dalam Persamaan x/2 + 3 = 7
Untuk mencari nilai x dalam persamaan x/2 + 3 = 7, kita ikuti langkah-langkah berikut:
- Kurangi 3 dari kedua ruas persamaan: x/2 + 3 – 3 = 7 – 3 ⇒ x/2 = 4
- Kalikan kedua ruas persamaan dengan 2: (x/2)
- 2 = 4
- 2 ⇒ x = 8
Dengan demikian, nilai x yang memenuhi persamaan x/2 + 3 = 7 adalah 8.
Menentukan Nilai x dalam Persamaan 4x + 1 = 9
Berikut langkah-langkah untuk menentukan nilai x dalam persamaan 4x + 1 = 9:
- Kurangi 1 dari kedua ruas persamaan: 4x + 1 – 1 = 9 – 1 ⇒ 4x = 8
- Bagi kedua ruas persamaan dengan 4: 4x / 4 = 8 / 4 ⇒ x = 2
Maka, nilai x yang memenuhi persamaan 4x + 1 = 9 adalah 2.
Menentukan Nilai x dalam Persamaan 5 – x = 2
Untuk menemukan nilai x dalam persamaan 5 – x = 2, kita dapat menggunakan dua metode:
| Metode | Langkah 1 | Langkah 2 | Hasil |
|---|---|---|---|
| Metode 1 (Mengisolasi x) | Kurangi 5 dari kedua ruas: -x = -3 | Kalikan kedua ruas dengan -1: x = 3 | x = 3 |
| Metode 2 (Memindahkan x) | Pindahkan x ke ruas kanan dan 2 ke ruas kiri: 5 – 2 = x | Hitung selisih: 3 = x | x = 3 |
Dengan kedua metode, nilai x yang memenuhi persamaan 5 – x = 2 adalah 3.
Menentukan Nilai x dalam Persamaan Kuadrat: Tentukan Nilai X Serta Jelaskan Alasanmu
Menentukan nilai x pada persamaan kuadrat merupakan keterampilan dasar dalam aljabar. Persamaan kuadrat, yang berbentuk ax² + bx + c = 0, memiliki berbagai metode penyelesaian, tergantung pada karakteristik persamaan tersebut. Berikut beberapa contoh penyelesaian persamaan kuadrat dan penjelasannya.
Nilai x pada x² + 5x + 6 = 0
Persamaan kuadrat x² + 5x + 6 = 0 dapat diselesaikan dengan pemfaktoran. Kita mencari dua bilangan yang jika dijumlahkan hasilnya 5 dan jika dikalikan hasilnya 6. Bilangan tersebut adalah 2 dan 3. Maka persamaan dapat difaktorkan menjadi (x + 2)(x + 3) = 0. Oleh karena itu, nilai x yang memenuhi persamaan adalah x = -2 atau x = -3.
Nilai x pada x² – 4x + 3 = 0
Persamaan x²
-4x + 3 = 0 juga dapat diselesaikan dengan pemfaktoran. Kita mencari dua bilangan yang jika dijumlahkan hasilnya -4 dan jika dikalikan hasilnya 3. Bilangan tersebut adalah -1 dan -3. Persamaan difaktorkan menjadi (x – 1)(x – 3) = 0. Akar-akar persamaan ini adalah x = 1 dan x = 3.
Kedua nilai ini mewakili titik potong grafik fungsi kuadrat dengan sumbu x.
Nilai x pada 2x² + 7x + 3 = 0
Untuk persamaan 2x² + 7x + 3 = 0, kita akan menggunakan rumus kuadratik:
x = [-b ± √(b²
-4ac)] / 2a
dengan a = 2, b = 7, dan c =
3. Substitusikan nilai-nilai tersebut ke dalam rumus:
x = [-7 ± √(7²
-4
– 2
– 3)] / (2
– 2) = [-7 ± √(49 – 24)] / 4 = [-7 ± √25] / 4 = [-7 ± 5] / 4
Maka, nilai x yang memenuhi adalah x = (-7 + 5) / 4 = -1/2 dan x = (-7 – 5) / 4 = -3.
Nilai x pada x² – 9 = 0
Persamaan x²
-9 = 0 dapat diselesaikan dengan metode selisih dua kuadrat. Persamaan tersebut dapat ditulis ulang sebagai x²
-3² = 0, yang kemudian difaktorkan menjadi (x – 3)(x + 3) = 0. Oleh karena itu, nilai x yang memenuhi adalah x = 3 atau x = -3. Metode ini dipilih karena persamaan tersebut merupakan bentuk selisih dua kuadrat yang mudah difaktorkan.
Nilai x dan Grafik Fungsi Kuadrat x² + 2x – 15 = 0
Persamaan x² + 2x – 15 = 0 dapat difaktorkan menjadi (x + 5)(x – 3) =
0. Dengan demikian, nilai x yang memenuhi adalah x = -5 atau x =
3. Grafik fungsi kuadrat y = x² + 2x – 15 merupakan parabola yang terbuka ke atas. Titik potong sumbu x berada pada x = -5 dan x =
3.
Titik puncak parabola dapat ditemukan dengan rumus x = -b/2a = -2/(2*1) = –
1. Substitusikan x = -1 ke dalam persamaan untuk mendapatkan nilai y: y = (-1)² + 2(-1)
-15 = -16. Jadi, titik puncak parabola berada di (-1, -16). Grafik tersebut simetris terhadap sumbu vertikal yang melalui titik puncak.
Menentukan Nilai x dalam Persamaan Linear Dua Variabel
Menentukan nilai x dan y dalam sistem persamaan linear dua variabel merupakan keterampilan dasar dalam aljabar. Kemampuan ini penting dalam berbagai bidang, mulai dari pemecahan masalah matematika sederhana hingga aplikasi di bidang teknik, ekonomi, dan ilmu komputer. Artikel ini akan membahas beberapa metode untuk menyelesaikan sistem persamaan linear dua variabel dan menentukan nilai x dan y.
Penyelesaian Sistem Persamaan 2x + y = 7 dan x – y = 2
Sistem persamaan 2x + y = 7 dan x – y = 2 dapat diselesaikan dengan metode eliminasi. Dengan menjumlahkan kedua persamaan, variabel y akan tereliminasi, menghasilkan 3x = 9, sehingga x = 3. Substitusikan nilai x = 3 ke salah satu persamaan (misalnya, x – y = 2), maka 3 – y = 2, sehingga y = 1.
Jadi, nilai x = 3 dan y = 1.
Penyelesaian Sistem Persamaan x + 3y = 10 dan 2x – y = 5, Tentukan nilai x serta jelaskan alasanmu
Sistem persamaan ini dapat diselesaikan dengan metode substitusi. Dari persamaan pertama, kita dapat menyatakan x dalam y: x = 10 – 3y. Substitusikan ekspresi ini ke persamaan kedua: 2(10 – 3y)
-y = 5. Sederhanakan persamaan tersebut untuk mendapatkan nilai y, kemudian substitusikan kembali ke salah satu persamaan awal untuk mendapatkan nilai x.
- 20 – 6y – y = 5
- -7y = -15
- y = 15/7
- Substitusikan y = 15/7 ke x = 10 – 3y:
- x = 10 – 3(15/7) = 10 – 45/7 = (70 – 45)/7 = 25/7
Jadi, nilai x = 25/7 dan y = 15/7.
Perbandingan Metode Substitusi dan Eliminasi pada Sistem Persamaan 3x + 2y = 11 dan x – y = 2
Kedua metode, substitusi dan eliminasi, dapat digunakan untuk menyelesaikan sistem persamaan 3x + 2y = 11 dan x – y =
2. Berikut perbandingannya:
- Metode Eliminasi: Kalikan persamaan kedua dengan 2, sehingga menjadi 2x – 2y = 4. Jumlahkan persamaan ini dengan persamaan pertama (3x + 2y = 11) untuk mengeliminasi y. Hasilnya adalah 5x = 15, sehingga x = 3. Substitusikan x = 3 ke salah satu persamaan awal untuk mendapatkan y = 1.
- Metode Substitusi: Dari persamaan kedua, nyatakan x dalam y: x = y +
2. Substitusikan ekspresi ini ke persamaan pertama: 3(y + 2) + 2y = 11. Sederhanakan persamaan ini untuk mendapatkan nilai y, lalu substitusikan kembali ke x = y + 2 untuk mendapatkan nilai x.
Kedua metode menghasilkan solusi yang sama (x = 3, y = 1). Pemilihan metode bergantung pada preferensi dan kemudahan perhitungan dalam kasus tertentu. Metode eliminasi seringkali lebih efisien jika koefisien variabel mudah dieliminasi, sedangkan metode substitusi lebih mudah jika salah satu variabel mudah diisolasi.
Penyelesaian Sistem Persamaan 4x – y = 9 dan x + 2y = 6
Sistem persamaan ini dapat diselesaikan dengan metode eliminasi. Kalikan persamaan kedua dengan 2, sehingga menjadi 2x + 4y = 12. Kemudian kalikan persamaan pertama dengan 4, sehingga menjadi 16x – 4y = 36. Jumlahkan kedua persamaan yang sudah dikalikan untuk mengeliminasi y, sehingga diperoleh 18x = 48, maka x = 8/3. Substitusikan nilai x ke salah satu persamaan awal untuk mendapatkan nilai y.
Representasi Grafik Sistem Persamaan x + y = 5 dan x – y = 1
Sistem persamaan x + y = 5 dan x – y = 1 dapat direpresentasikan secara grafik. Kedua persamaan tersebut merupakan persamaan garis lurus. Titik potong kedua garis tersebut merepresentasikan solusi dari sistem persamaan.
Dengan menggambarkan kedua garis, titik potongnya akan menunjukkan nilai x dan y yang memenuhi kedua persamaan. Secara visual, titik potong tersebut dapat ditentukan dengan melihat koordinat titik perpotongan kedua garis pada grafik. Perhitungan aljabar (misalnya, dengan metode eliminasi atau substitusi) akan mengkonfirmasi koordinat titik potong tersebut.
Menentukan Nilai x dalam Persamaan Lainnya
Menentukan nilai x dalam berbagai jenis persamaan matematika merupakan keterampilan fundamental dalam aljabar. Kemampuan ini penting untuk memecahkan masalah dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan ilmu komputer. Berikut ini akan dijelaskan beberapa contoh penentuan nilai x dalam berbagai jenis persamaan, meliputi pertidaksamaan, persamaan nilai mutlak, persamaan eksponensial, dan persamaan logaritma.
Penyelesaian Pertidaksamaan Linear
Pertidaksamaan linear melibatkan perbandingan antara dua ekspresi aljabar. Untuk menentukan nilai x yang memenuhi pertidaksamaan, kita perlu melakukan operasi aljabar untuk mengisolasi variabel x. Berikut contohnya:
- 2x + 3 > 7
- Kurangi 3 dari kedua ruas: 2x > 4
- Bagi kedua ruas dengan 2: x > 2
Penyelesaian pertidaksamaan ini adalah x > 2. Pada garis bilangan, ini direpresentasikan dengan sebuah titik terbuka pada angka 2 dan sebuah garis panah mengarah ke kanan, menunjukkan semua nilai x yang lebih besar dari 2.
Penyelesaian Pertidaksamaan Linear Lainnya
Berikut penyelesaian pertidaksamaan 5x – 2 ≤ 13:
- Tambahkan 2 ke kedua ruas: 5x ≤ 15
- Bagi kedua ruas dengan 5: x ≤ 3
Alasannya sederhana: dengan mengikuti langkah-langkah aljabar yang tepat, kita berhasil mengisolasi x dan menemukan batas nilai x yang memenuhi pertidaksamaan.
Menentukan Nilai x dalam Persamaan Nilai Mutlak
Persamaan nilai mutlak melibatkan fungsi nilai mutlak, yang selalu menghasilkan nilai non-negatif. Untuk menyelesaikan persamaan nilai mutlak, kita perlu mempertimbangkan dua kemungkinan kasus, yaitu ketika ekspresi di dalam nilai mutlak positif dan ketika ekspresi tersebut negatif.
Sebagai contoh, untuk persamaan |x – 3| = 5, kita memiliki dua kasus:
- Kasus 1: x – 3 = 5 ⇒ x = 8
- Kasus 2: x – 3 = -5 ⇒ x = -2
Oleh karena itu, nilai x yang memenuhi persamaan adalah x = 8 atau x = -2.
Menentukan Nilai x dalam Persamaan Eksponensial
Persamaan eksponensial melibatkan variabel x sebagai eksponen. Untuk menyelesaikannya, kita seringkali perlu menggunakan sifat-sifat eksponen atau mengubah basis agar sama.
Misalnya, untuk persamaan 2ˣ = 8, kita dapat menulis ulang 8 sebagai 2³:
2ˣ = 2³
Karena basisnya sama, maka eksponennya juga harus sama. Oleh karena itu, x = 3.
Menentukan Nilai x dalam Persamaan Logaritma
Persamaan logaritma melibatkan fungsi logaritma. Untuk menyelesaikannya, kita dapat menggunakan definisi logaritma atau sifat-sifat logaritma.
Sebagai contoh, untuk persamaan log₂(x) = 3, berdasarkan definisi logaritma, kita dapat menulis ulang persamaan tersebut sebagai:
2³ = x
Oleh karena itu, x = 8.
Penutup
Menentukan nilai x, terlepas dari kompleksitas persamaannya, merupakan keterampilan fundamental dalam matematika. Melalui pemahaman yang sistematis terhadap berbagai metode penyelesaian, dari manipulasi aljabar sederhana hingga penerapan rumus kuadratik dan metode substitusi/eliminasi, kita dapat menguasai teknik untuk menemukan solusi. Kemampuan ini bukan hanya penting untuk menyelesaikan soal-soal matematika, tetapi juga merupakan dasar untuk memecahkan masalah dalam berbagai bidang ilmu dan kehidupan sehari-hari.